Reading: Financing and Experimentation

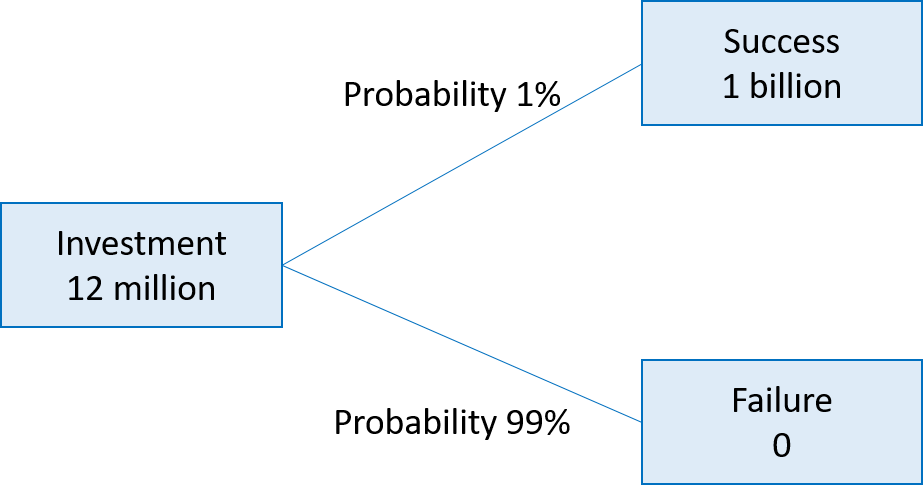
Consider a startup company that wants to launch a new drug against Alzheimer's disease:

• The required investment is 12 million today.
• There is a 1% probability that the drug will be successful. If so, the present value of all future cash flows (excluding today's investment) is 1 billion. 
• There is a 99% probability that the drug will fail and, therefore, have a value of 0.

 Should we invest?

The following figure summarizes the basic setup of the project:

Because the success probability is so low, it is not worthwhile to undertake the project: The expected value of the success scenario is only 10 million (1% probability to get 1 billion), which is 2 million short of the required investment of 12 million. Formally, the project's NPV is -2 million:

\( NPV = - 12 + 0.01 \times 1000 + 0.99 \times 0 = -12 + 10 = - 2 \)

Note, however, that the project is not necessarily bad. Similar to a lottery ticket, there is a chance that a comparatively small investment of 12 million can be transformed into a massive payout of 1 billion. The problem simply is that the probability of success is too low to justify today's investment.

However, unlike a lottery ticket, the success probability of the new drug (or any other risky endeavor) might not be set in stone. It is the best possible assumption based on today's available information. But what if one could conduct additional experiments to learn more about the success probability of the drug before committing to the investment of 12 million?

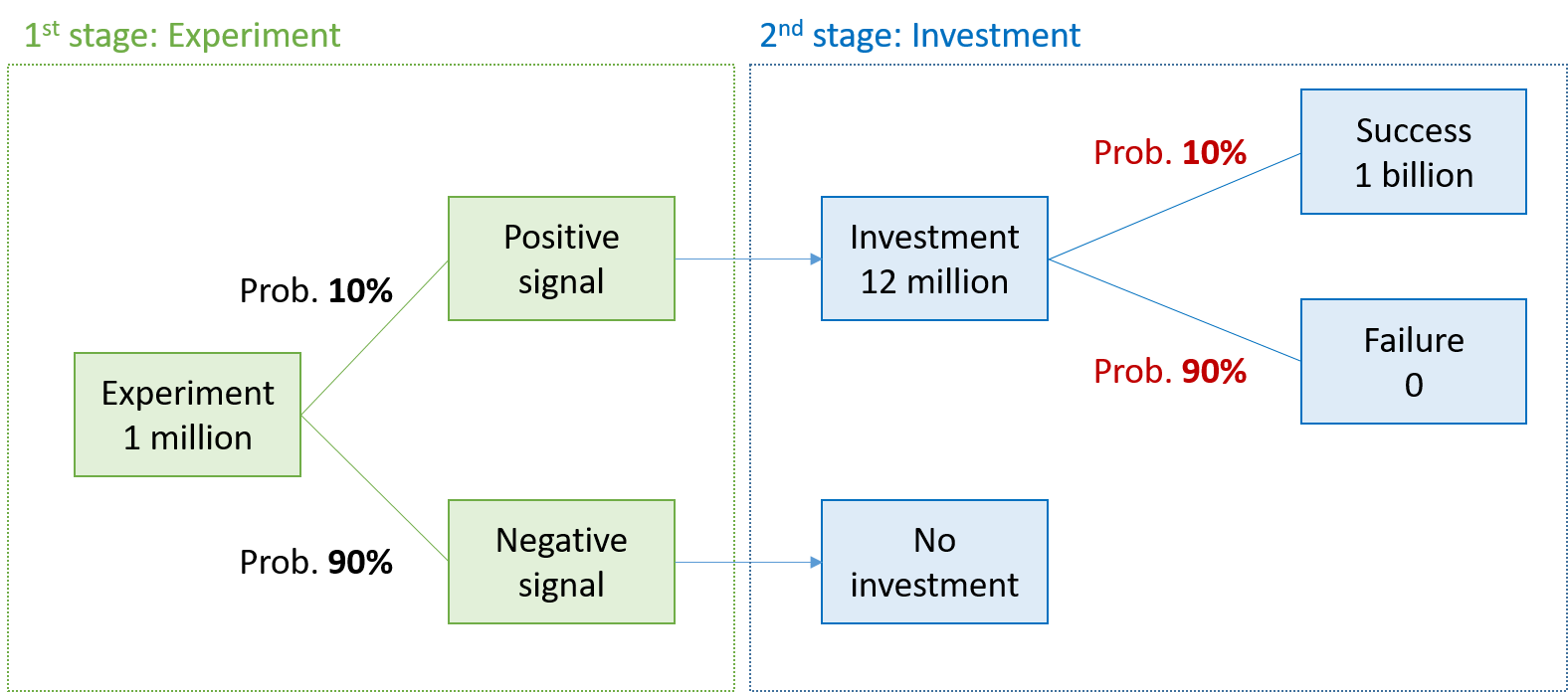
For the sake of illustration, let us assume the following:

• The ability to successfully cross the blood-brain barrier is a key uncertainty of the envisioned drug and a main contributor to the low overall success probability.
• For an additional investment of 1 million, the firm could run an experiment that sheds more light on the drug's ability to cross the blood-brain barrier. The experiment has the following characteristics:
  • There is a 10% probability that it will produce a positive signal. If so, the success probability the drug increases from 1% to 10%.
  • There is a 90% probability that the experiment will send a negative signal. If so, the drug will fail.

How does the option to conduct an additional experiment affect the value of the drug and our investment decision? The following graph shows the new constellation with the additional experiment. Before deciding about the actual investment of 12 million (blue area), we can conduct the described experiment (green area). The main implication of this experiment is that, if successful (positive signal), it improves the success probability of the second investment from 1% to 10%:

To value the drug with the preceding experiment, it is best to solve the above decision tree recursively:

• If the experiment is successful, the 2^nd stage investment of 12 million unlocks a drug that is valued at 1 billion with probability 10% and 0 otherwise. Hence, in the case of a successful initial experiment, the expected value of the drug is 100 million and the NPV is 88 million (= -12 + 0.1 × 1'000).
• If the experiment fails, we do not proceed with the investment and the value of the drug is 0.

The probability of a successful initial experiment is 10%, according to our assumptions. Consequently, after the experiment, the NPV of the drug will be 88 million with probability 10% and 0 with probability 90%. The expected value, therefore, is 8.8 million (= 0.1×88 + 0.9×0). The cost of the experiment is 1 million, so that the overall NPV of the drug project is 7.8 million:

\(NPV_{\text{with experiment}}=-1 + 0.1 \times 88 + 0.9 \times 0 = -1 + 8.8 = 7.8 \) million. 

Thanks to the additional experiment, the NPV of the project therefore increases from -2 million to 7.8 million. This is quite a remarkable result: The NPV goes up, even though the potential value of the drug remains the same (1 billion), we incur additional costs (1 million), and the overall success probability of the drug is still only 1% (0.1 × 0.1 = 0.01)!

How is this possible? The answer is relatively simple: Failure has become cheaper. Instead of 12 million, we now have to invest only 1 million to learn with high certainty whether the project will fail. This allows us to considerably reduce the downside risk, which makes the project overall more valuable. Whereas the project was not feasible with a full upfront investment, it is now an attractive investment thanks to the initial experiment and the associated staged financing.