Reading: Startups as Real Options

Let us formalize the above analysis a bit so that it will be easier to apply it in different settings. We use the following notation:

• S = Value of the underlying asset
• X = Required investment
• up = State of the world where the value of the underlying asset increases
• down = State of the world where the value of the underlying asset decreases
• u = Factor of the price increase
• d = Factor of the price decrease
• π = risk-neutral probability of the scenario "up"
• R = risk-free rate of return
• C = Value of the option.

 
Using this notation, we can depect the two trees from above as follows:
 

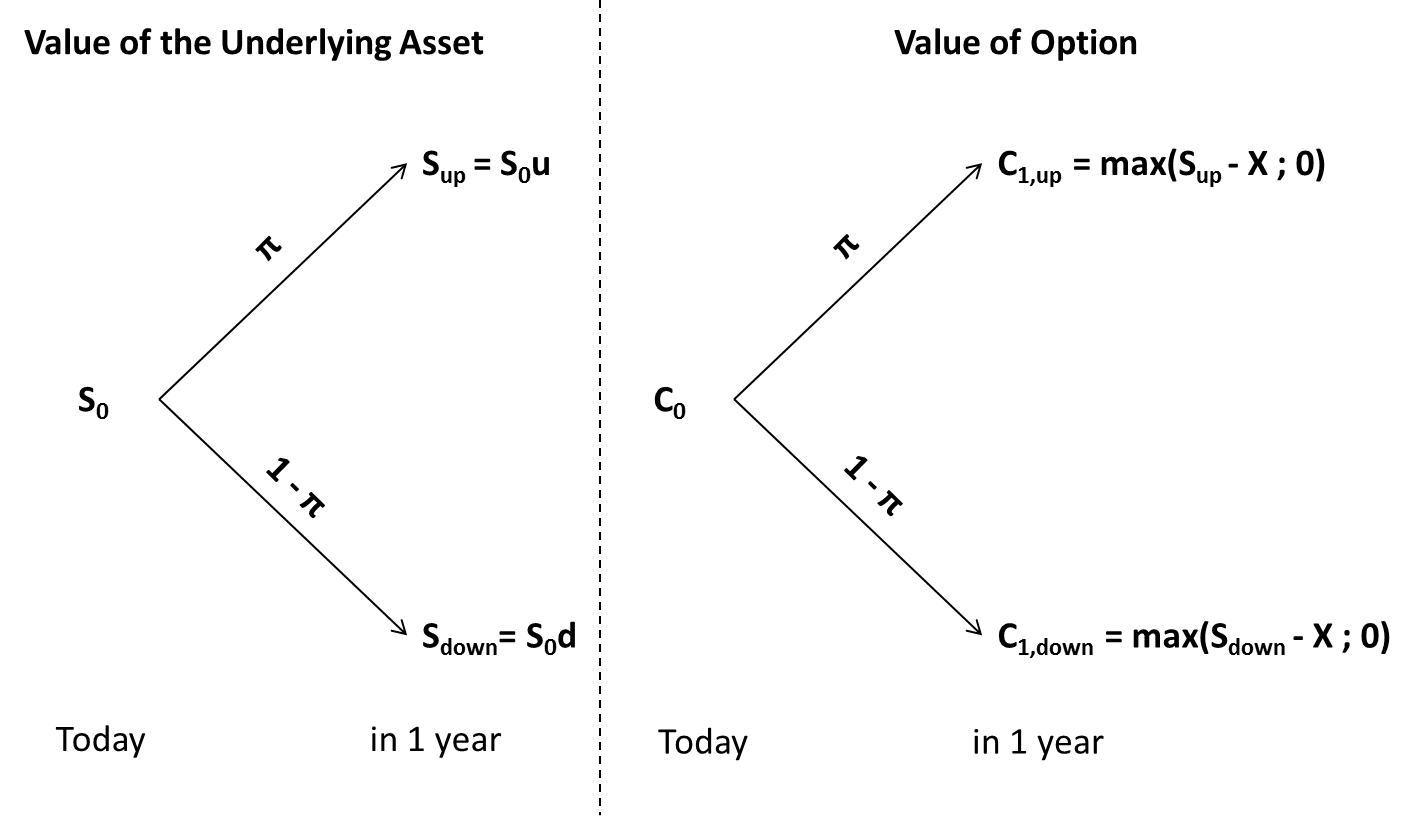
In "words":

• The value of the underlying asset either increases by a factor u to S_up or drops by a factor d to S_down. The corresponding probabilities are π and (1-π), respectively.
• The value of the right to invest is a bit trickier. We invest if the value of the underlying asset (S) exceeds the required investment (X). In this case, the value of the option is (S - X). Otherwise, we do not invest and the value of the option is 0. So we pick whatever is larger from (S - X) and 0. Put differently, we pick the maximum of (S - X) and 0. The formal way to write this is max(S-X; 0).

We have argued that the current value of the underlying asset (S₀) corresponds to the present value of the expected future value of the underlying asset. Consequently:

\( S_0 = \frac{\pi \times S_0 \times u + (1-\pi) \times S_0 \times d}{1+R} \).

This allows us to back out π, the risk-neutral probability of the "up" scenario:

\( \pi = \frac{ (1+R) - d}{u - d} \)

Once we have backed out this probability, we can value the option:

\(C_0 = \pi \times \frac{C_{up}}{1+R} + (1-\pi) \times \frac{C_{down}}{1+R} \).

In our example, we had S₀ = 100, u = 1.5, S_up = 150, d = 0.5, S_down = 50, and R = 5%. Consequently, the risk-neutral probability of the up-scenario is 55%:
 

\( \pi = \frac{ (1+R) - d}{(u - d} = \frac{ 1.05 - 0.5}{1.5 - 0.5} = 0.55 \)

We have also seen that the option payoffs in the two scenarios are:

C_up = max(S_up - X; 0) = max(150 - 120; 0) = 30

C_down = max(S_down - X; 0) = max(50 - 120; 0) = 0.

So whe can value the option as follows: 

\(C_0 = \pi \times \frac{C_{up}}{1+R} + (1-\pi) \times \frac{C_{down}}{1+R} = 0.55 \times \frac{30}{1.05} + 0.45 \times \frac{0}{1.05} = 15.7 \) million.