Reading: Startups as Real Options

Let's look at another example to practice the binomial valuation. In this example, the investment opportunity lasts two years. So the owner of that opportunity has to decide whether she wants to invest today, in 1 year, or in 2 years.

Using the notation from before, let us assume the following:

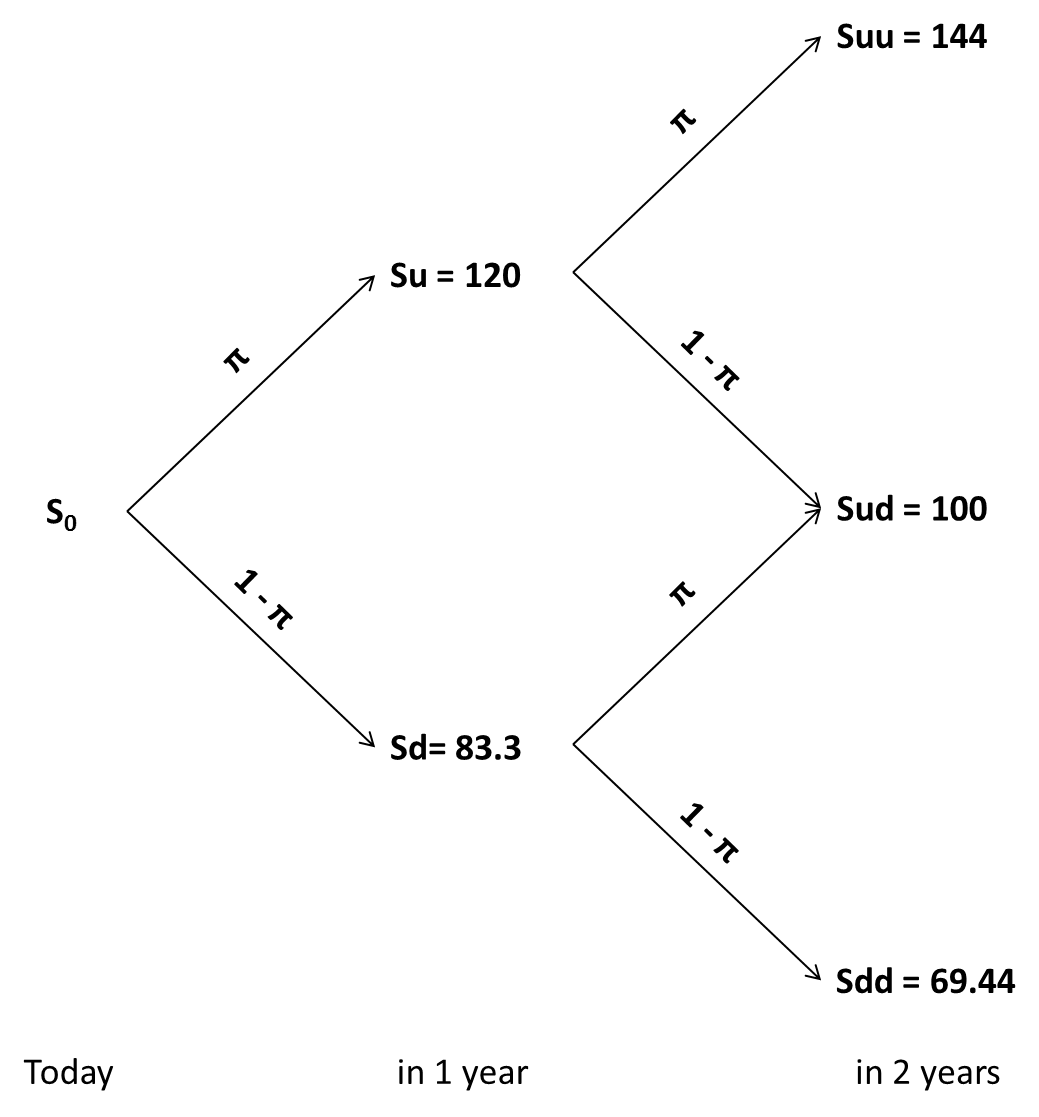
• We can invest 90 (X) in a project with a current value of 100 (S)
• The value of the project can either increase by a factor 1.2 (u) or drop by the same factor (d = 1/1.2 = 0.8333)
• The risk-free rate of return is 5%
• The investment opportunity lasts 2 years.

The following tree depicts the price development of the underlying asset over the next two years:

We can find the risk-neutral probability π with the expression from the previous page:

 
\( \pi = \frac{ (1+R) - d}{u - d} = \frac{1.05 - 0.833}{1.2 - 0.833} = 0.59 \)

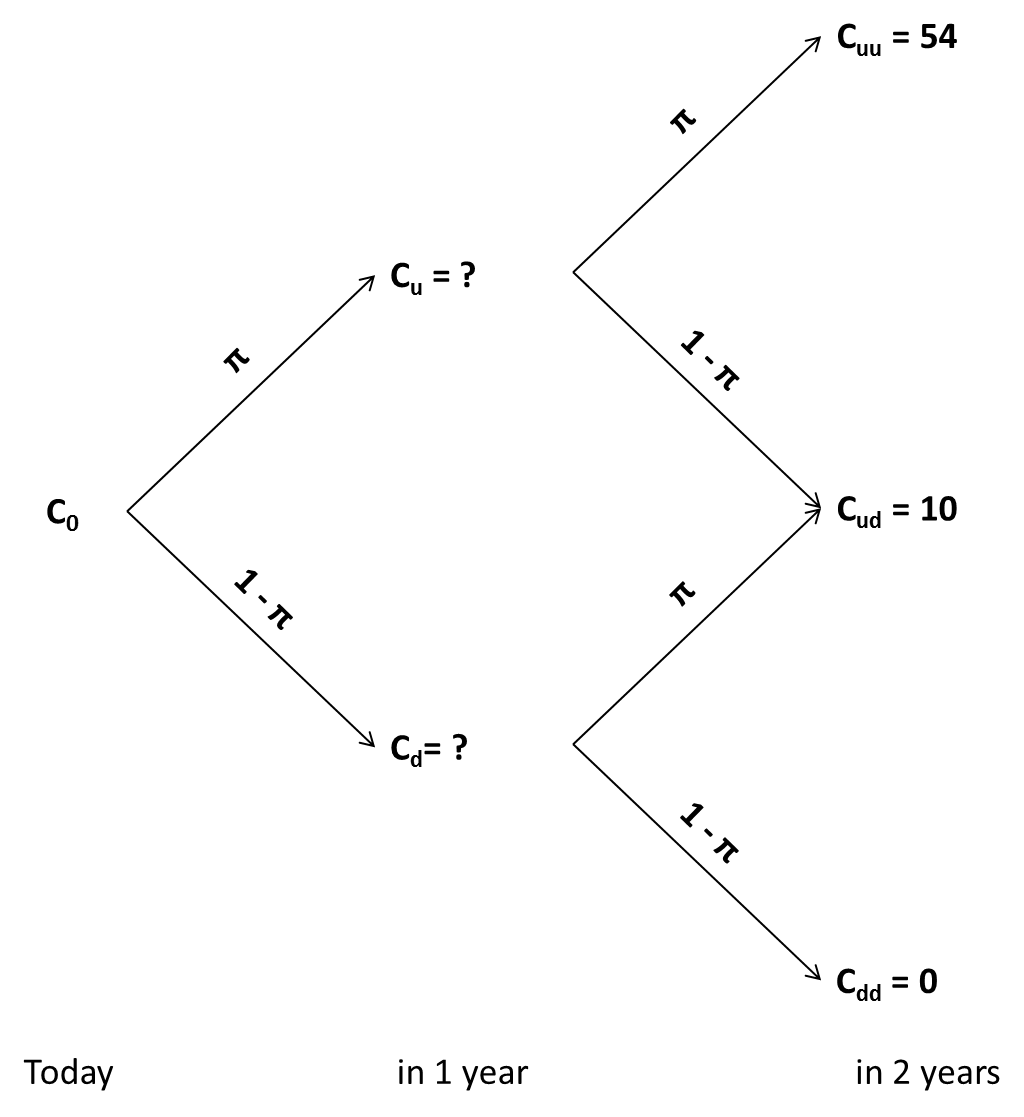
Given that the required investment is 90, we can also derive the option payoffs at the end of year 2 as follows:

Now how to value this tree? Very similarly to what we did before. Let us put ourselves in the "up" scenario at the end of year 1:

• We know that the value of the underlying asset in this scenario is 120. We could "exercise" the investment opportunity and invest the 90 million in 1 year. If we do so, the value we capture in 1 year in the "up" scenario will be 30 million [= -90 + 120].
• Alternatively, we can postpone the investment by an additional year to the end of year 2. The above tree shows us that postponing the investment will give us a payoff of 54 with probability π and a payoff of 10 with probability (1-π). At the end of year 1, the present value of these expected payoffs is (using the expressions from the previous page) 34.28 million:
   
  \(C_{u,postpone} = \pi \times \frac{C_{uu}}{1+R} + (1-\pi) \times \frac{C_{ud}}{1+R} = 0.59 \times \frac{54}{1.05} + (1-0.59) \times \frac{10}{1.05} = 34.28 \) million.
   
• Put differently, if we end up in the "up" scenario in 1 year, it is better NOT to exercise the option. The corresponding value (30 million) is smaller than the value we unlock by postponing the investment decision by one more year (34.28 million).
• The value of the investment opportunity in the "up" scenario in 1 year is consequently 34.28 million.

If we end up in the "down" scenario in 1 year, the situation is at follows:

• In principle, we could exercise the investment opportunity in 1 year. However, doing so would have a negative value, since the required investment (90 million) exceeds the value of the underlying asset in the "down" scenario (83.3 million).
• Postponing the decision will generate an project value of 10 million with probability (π) and a project value of 0 with proability (1-π). Consequently, at the end of year 1, the present value of these expected payoffs is 5.62 million.
   
  \(C_{d,postpone} = \pi \times \frac{C_{ud}}{1+R} + (1-\pi) \times \frac{C_{dd}}{1+R} = 0.59 \times \frac{10}{1.05} + (1-0.59) \times \frac{0}{1.05} = 5.62 \) million.
   
• The value of the investment opportunity in the "down" scenario in 1 year is consequently 5.62 million.

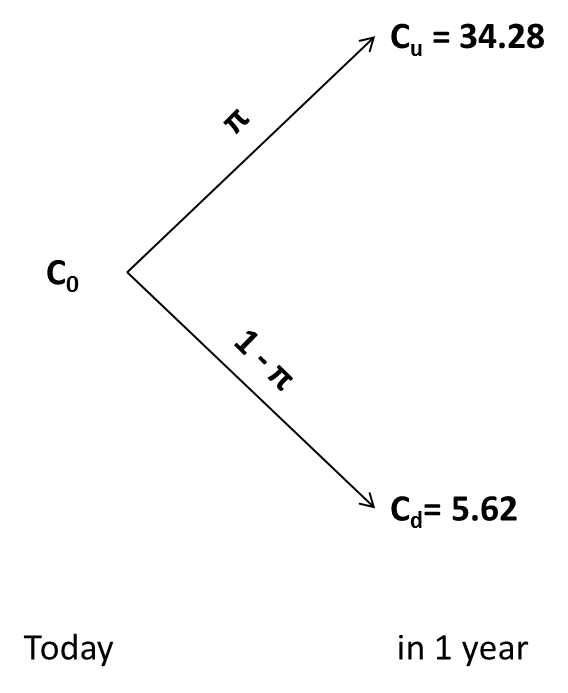
With these computations, we could simplify the option valuation tree as follows:

With this information, we are now ready to compute the current value of the investment opportunity. Today, we face the same decision as in year 1: Should we invest or postpone the investment decision?

• With a current value of the underlying asset of 100 million, the decision to invest today would have a NPV of 10 million [= -90 + 100].
• In contrast, if we postpone that decision by 1 year, the above tree shows us that the value in 1 year will be either 34.28 or 5.62. The probability-weighted present value of these payoffs is 21.49 million:
   
  \(C_{0,postpone} = \pi \times \frac{C_{u}}{1+R} + (1-\pi) \times \frac{C_{d}}{1+R} = 0.59 \times \frac{34.28}{1.05} + (1-0.59) \times \frac{5.62}{1.05} = 21.49 \) million.
   
• Consequently, it is financially more attractive to not invest today.

In sum, we have used the binomial method to value a "simple" investment opportunity that lasts 2 years. Our computations imply that the value of this opportunity is 21.49 million today. Our analysis also implies that we should postpone the investment decision as far into the future as possible:

• Today, it is optimal to postpone (Value = 21.49 million) rather than to invest (Value = 10 million)
• Also in year 1, regardless of whether we end up in the "up" or the "down" scenario, it will be optimal to postpone.

The finding that we should not exercise such options early is a general finding for options on asset that do not pay any dividends during the lifetime of the option. In reality, especially in the context of real options, the assumption of zero dividends might be questionable. In the following section, we therefore revise the example and investigate how a dividend payment could alter our conclusions.