Reading: Startups as Real Options

Now let us investigate how the analysis changes when we have investment opportunities that offer dividend payments during their lifetime. Such a dividend payment could be the foregone cash flow from year 1 if we do not invest today.

Let us go back to the previous example and assume that the investment opportunity will pay a dividend of 20 million in 1 year.

A dividend payment of 20 million implies that the value of the asset will drop by that amount right after the payment of the dividend. The following graph summarizes the possible price development of the underlying asset based on the revised scenario. For reading convenience, we drop the probabilities of the various branches from the graph (π and 1-π):

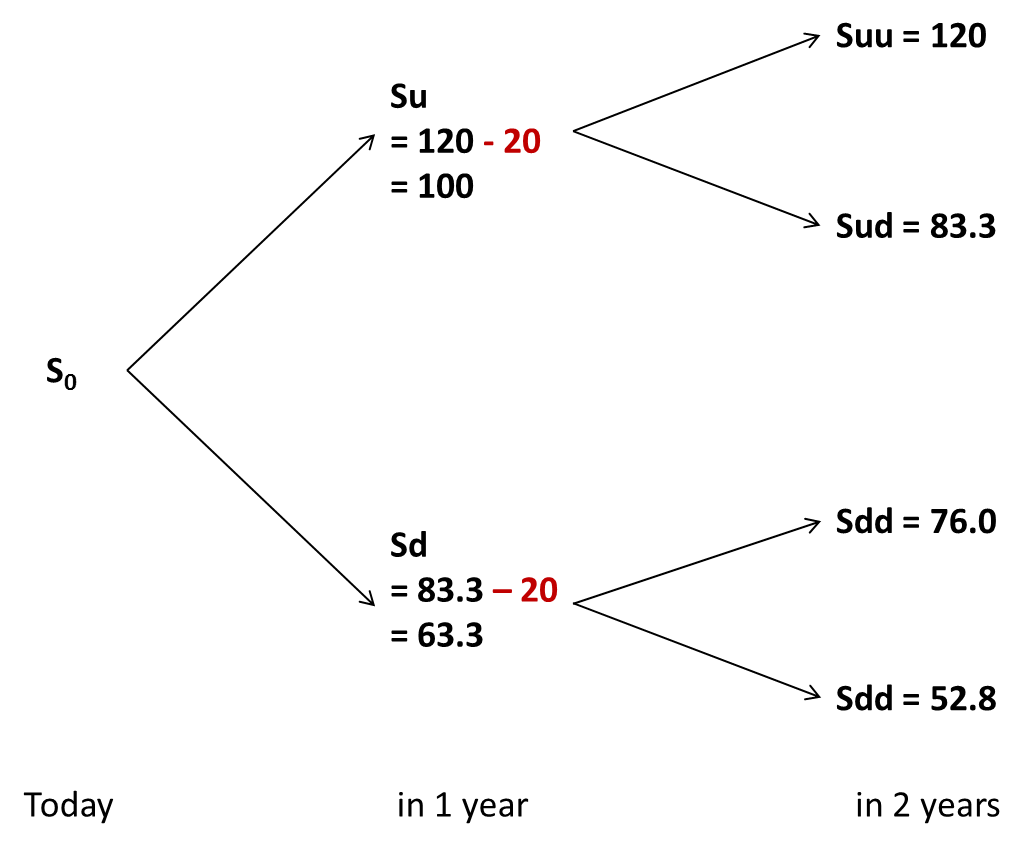
In the "up" scenario, the asset value increases to 120 in 1 year. As the asset then pays a dividend of 20, its value drops back to 100. Subsequently, the asset value will then either increase to 120 or drop to 83.3.

In contrast, if the asset value drops to 83.3 during the first year, the dividend payment of 20 will further reduce the value to 63.3. Consequently, in year 2, the value will be either 76 [= 63.3 × 1.2] or 52.8 [= 63.3 / 1.2].

As the owner of the option, we have to decide whether we want to exercise the investment opportunity in 1 year right before the dividend payment or whether we want to forego that dividend payment and postpone the investment decision.

Postponing the investment decision to year 2 brings the following option values at the end of year 2:
 

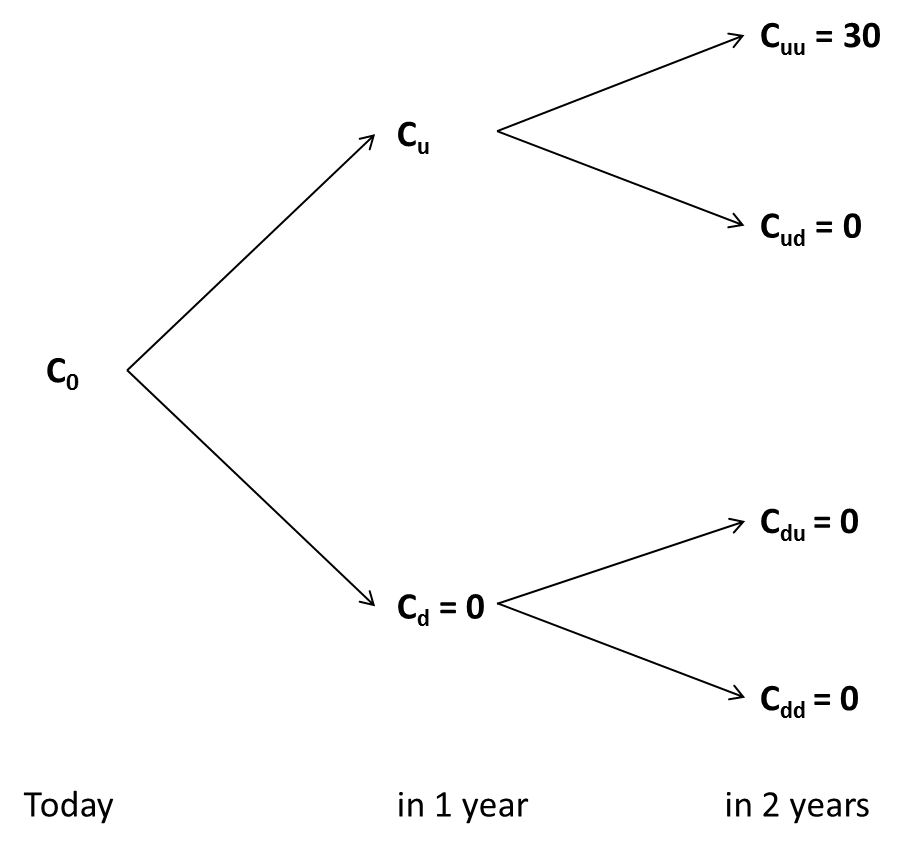
If the value of the underlying asset drops to 83.3, it falls below the necessary investment of 90 and will not recover thereafter. Therefore, we will never exercise the option, which is why it has a value of 0 in this state of the world (C_d = 0).

But what about the "up" scenario? Here we have to decide between two alternatives:

• Exercise the investment opportunity right before the first dividend payment. In this case, the value of the investment opportunity will be 30 million [= 120 - 90].
• Forego the first dividend and postpone the investment decision until year 2. In this case, the value of the option at the end of year 1 will be 16.9 million, following the exact same procedure as in the previous example:
   
  \(C_{u,postpone} = \pi \times \frac{C_{uu}}{1+R} + (1-\pi) \times \frac{C_{ud}}{1+R} = 0.59 \times \frac{30}{1.05} + (1-0.59) \times \frac{0}{1.05} = 16.9 \) million.
   

Because of the large dividend payment in year 1, it now makes sense to exercise the option early in the "up" scenario! Consequently the management implications of this analysis are as follows:

• If the value of the underlying asset increases, do not further postpone the investment decision and exercise the option right before the first dividend payment.
• If the value of the underlying asset drops, the investment opportunity will be worthles.