Reading: Startups as Real Options

The last option pricing approach that we consider here is the Black-Scholes (or Black-Scholes-Merton) valuation model. In a nutshell, this model is a very refined version of the binomial tree approach from the previous chapter. Under a set of (rather strict) assumptions, Black, Scholes, and Merton showed in the late 1970ies that the binomial option pricing model converges on the following pricing formulas, which are based on the same six value drivers as the binomial tree model:

• S: Current value of the underlying asset
• X: Exercise price; Price at which we can buy (call option) or sell (put option) the underlying asset
• T-t: Time to maturity; For how many periods the right is valid
• r: Risk-free rate of return in continuous compounding (r = ln(1+R))
• y: Dividend payments of the underlying asset (in continuous compounding)
• σ: Volatility of the return of the underlying asset (i.e., to what extent we expect the value of the underlying asset to fluctuate in the future).

Value of a call option (c):

\( c = S \times e^{-y(T-t)} \times N(d_1) - X \times e^{-r(T-t)} \times N(d_2) \)

Value of a put option (p):

\( p = X \times e^{-r(T-t)} \times N(-d_2) - S \times e^{-y(T-t)} \times N(-d_1) \)

With:

\( d_1 = \frac{ln(S/X)+(r-y+\sigma^2/2) \times (T-t)}{\sigma \times \sqrt{T-t}} \)

\( d_2 = d_1 - \sigma \times \sqrt{T-t} \)

N(d.) = Probability that a standard normal variable is smaller than the value specified by d. It is the shaded surface under the standard normal distribution from -∞ to d.

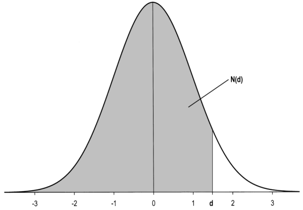
For the application in this course, we should not worry too much about these formulas. There are countless websites that help you apply these formulas. For your convenience, we have also prepared a simple Excel file that does the necessary computations for you. It is available for download here.

Still, it is important to understand what assumptions we have to make when using the Black-Scholes-Merton model as well as the other option pricing approaches, especially in the context of real options. We will get back to this point further down. First, let us practice the use of the Black-Scholes-Merton model a bit.

Example 1

You have the opportunity to buy a licence to produce a new experimental airplane. To buy the licence, you have to pay 15 million upfront. Once you own the license, you can then decide whether you want to invest in the production of the plane or not. The necessary investment to start production is 80 million. According to your own market analysis, the present value of all future cash flows you can earn with the airplane is 90 million. However, there is a great deal of uncertainty associated with the future development of this value. For example, the airplane has not yet received FAA approval, and you are not quite sure how competitors will react. All in all, you assume that the volatility of the value change is as high as 40%. We ignore "dividend payments" for the time being. You can start production (i.e., invest 80 million) either today or in 1 year. The risk-free rate of return (discrete compounding is 3%).

With this information, let us try to value the project.

First, let us assess whether it makes sense to buy the license if we make the investment decision today. In this case, the NPV of the project is:

NPV_{Decide today} = -Cost of License - Investment + PV(FCF) = -15 - 80 + 90 = -5 million.

If we have to make the investment decision today, it is not worthwhile to buy the license. The reason is that the cost of the license and the required investment exceed the present value of all future expected cash flows by 5 million.

But what if we postpone the investment decision by 1 year? By doing so, we buy ourselves time to observe how the market evolves. For example, we will learn if the plane receives FAA approval, if competitors plan to lauch similar products, etc. If in 1 year, we observe that the market has developed favorably, we invest. If not, we don't invest. Put differently, the license constitutes a call option on the airplane project. The question is whether the value of this call option justifies the price of the license of 15 million. This is what we have to figure out. To feed the option pricing model, we have the following parameters:

• S = 90
• X = 80
• T-t = 1 year
• R = 3% with discrete compounding (note that the Excel file converts this discrete return into a continuous return for the computations)
• y = 0
• σ = 40%.

We can plug these values in the above equations or in the provided Excel file:

The resulting value of the call option (c) is 20.33 million. Put differently, the right (but not the obligation) to start the production of the airplane in 1 year currently has a value of 20 million. The seller of the license only wants 15 million. Consequently, the NPV of the license purchase is 5.33 million:

NPV License = -Price of License + Value of License = -15 + 20.33 = 5.33 million.

Example 2:

A company has raised 2 million today for an investment that it plans to conduct in 2 years. The capital is currently invested in the financial market. Now the management wants to protect the capital against major losses. In particular, it wants to make sure that the value of the investment does not drop below 1.8 million in 2 years. The volatility of the investment is 15%, the risk-free rate of return is 3% (discrete compounding) and the investment pays an annual dividend of 2% (discrete compounding).

Based on this information, how much will a protection against major losses cost?

In our option terminology, the company is looking for a right to sell the investment in 2 years at a price of 1.8 million. Consequently, we are dealing with a put option with the following characteristics:

• S = 2 million
• X = 1.8 million
• T-t = 2 years
• R = 3% with discrete compounding (note that the Excel file converts this discrete return into a continuous return for the computations)
• y = 2% with discrete compounding (Excel will convert this into continuous compounding) 
• σ = 15%.

If we plug these values in the provided Excel file, we find (all values in 1'000):

Consequently, the value of the put option with the desired characteristics is roughly 66'000. Put differently, the insurance of the portfolio against major losses over the next 2 years will cost the company 66'000 today.