Reading: Startups as Real Options

The previous examples have illustrated the use of option pricing in situations where we can buy an asset (e.g., an investment opportunity). These are so-called Call Options. As we have discussed in the introductory chapter, managerial flexibility can also mean that we can dispose of an asset or a project. The right to sell something is called a Put Option.

In this section, we illustrate how we can use the same logic as before to value such put options. For the sake of brevity we use a right to sell on an underlying asset that does not pay any dividends:

Suppose we own a piece of land on which we want to search for gold. The current value of the land (S) is 10 million. We have already contracted a study team to explore whether there is gold in the ground. If there is gold, the value of the property increases to 100 million (u = 10). If not, it drops to 2 million (d = 0.2). The previous owner has granted us the right to sell him back the land at a price of 6 million (X). The risk-free rate of return is 5%. What's the value of this right to sell the land back to the previous owner (put option)?

The following graph summarizes the situation:

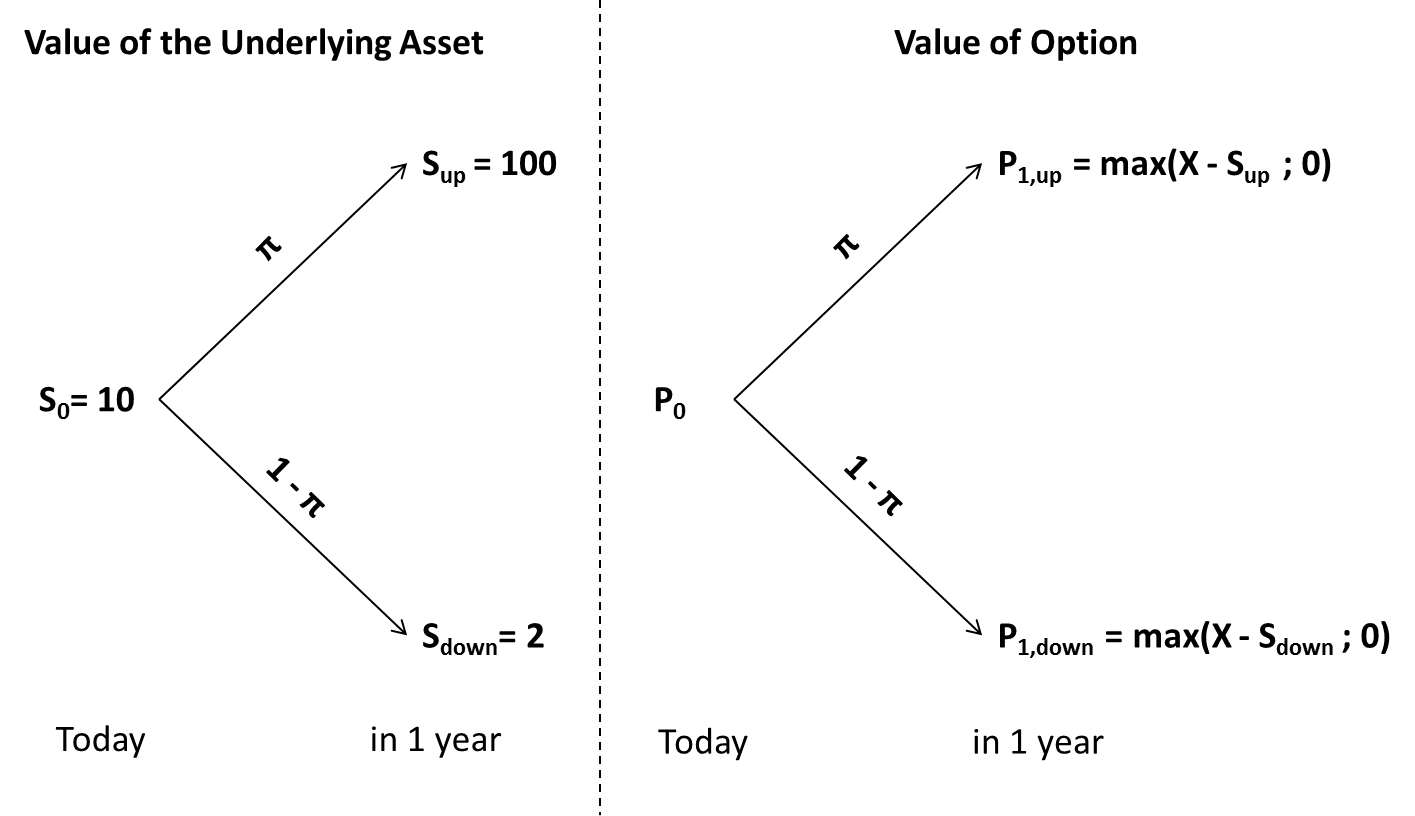
The first thing we can do is back out the risk-neutral probability of an increase in the asset value, using the exact same procedure as before:

\( \pi = \frac{ (1+R) - d}{u - d} = \frac{ 1.05 - 0.2}{10 - 0.2} = 0.0867 \)

The probability of a price increase to 100 million is therefore only 8.67%.

Now what's the payoff of the right to sell in 1 year?

• If the value of the land increases to 100 million in 1 year because there is gold, we will most likely not want to sell it back to the previous owner for 6 million. Consequently, the right to sell will be worthless (P_1,up = 0)
• If, in contrast, the value of the land drops to 2 million, selling it back to the previous owner for 6 million is attractive. In this case, the right to sell will have a value of 4 million, i.e., how much more we get when selling it to the previous owner (6 million) compared to selling it on the market (2 million). P_1,down = 4 million.

With this information, we can now value the put option: In 1 year, it will be worthless with probability 8.67% or have a value of 4 million with probability 91.33%:

\( P_0 = \pi \times \frac{P_{1,up}}{1+R} + (1-\pi) \times \frac{P_{1,down}}{1+R} = 0.0867 \times \frac{0}{1.05} + 0.9133 \times \frac{4}{1.05} = 3.48 \) million.

Based on this information, the right to sell therefore has a value of 3.48 million.