Reading: Startups as Real Options
6. Theory vs. Practice
In the previous chapters, we have looked at the most popular methods to value options. It is important to note that these models only hold under a set or rather restrictive assumptions, which are hardly ever met in practice --- especially in the context of real options. It would go beyond the scope of this module to discuss all the necessary assumptions in detail. Instead, we focus on some of the key assumptions that seem particularly relevant in the context of real options. For example:
- All investors can borrow and lend money at the risk-free rate of return.
- There are no arbitrage opportunities.
- The underlying asset can be bought and sold at any amount (even fractional amounts).
- Selling at any amount also means that short-selling is possible (sell the asset without actually owning it).
- There is an active market for the option itself.
- The markets are frictionless (transactions do not incur any fees or costs).
- The value development of the underlying asset follows a continuous random walk.
- The cost of exercising the option is "known."
- Investors are risk neutral.
Why are these assumptions so important? Because only when these assumptions are met, we can be confident that the theoretical value of an option also correponds to the actual price of that option.
Let us go back to our initial example of a binomial tree valuation. There, we have considered an underlying asset with a current value of 100 million and a possible future value of either 150 or 50 million. We valued the right to buy this asset at a price of 120 in 1 year. Using the binomial method, we have figured out that today's value of that right must be 15.7 million. The following graph summarizes the main considerations of that valuation problem:
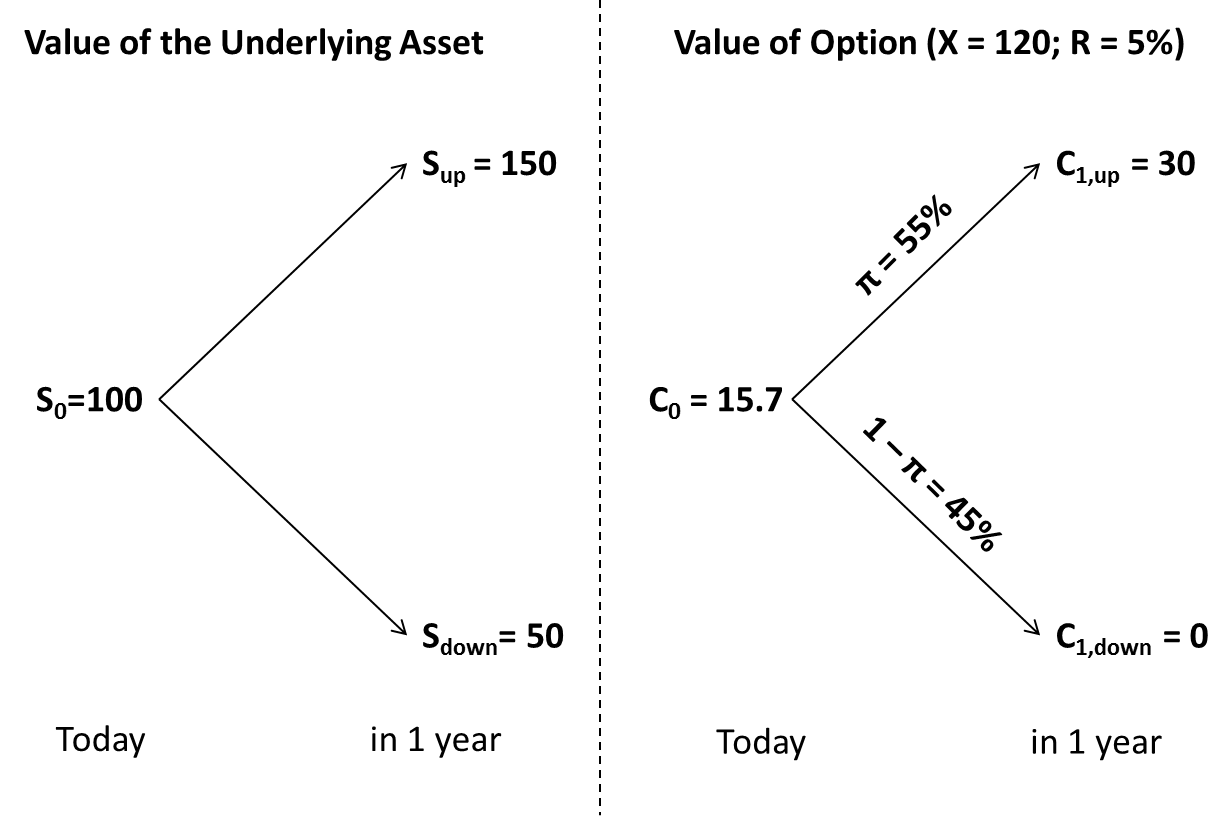
But how do we know that the price of this option will actually be 15.7 million?
The answer is that if the actual price differed materially from 15.7 million, investors would swamp the market to exploit the price difference. How could they do that?
The trick is to use existing financial instruments for which we observe a market price today to construct a portfolio that generates the exact same future payoffs as our option in question. Because we replicate the future payoff of another financial instrument, this portfolio is often called the replicating portfolio. The financial instruments we use to build the replicating portfolio are the underlying asset itself (with a current value S = 100) as well as risk-free borrowing and lending at 5%.
Remember from before that the option's future payoffs are as follows:
- If the value of the asset goes up (Sup = 150), the option payoff (Cup) will be 30
- If the value of the asset goes down (Sdown = 50), the option payoff (Cdown) will be 0
So what we need to now is combine the underlying assets and risk free borrowing/lending in a portfolio such that it produces the exact same future payoffs. To show how this works, let us use the following notation:
- The greek letter "delta" Δ denotes the units of asset S we buy today.
- B denots the amount of money we invest/borrow today until maturity (1 year) .
Today's value of our replicating portfolio, therefore, is Δ×S0 + B. In one year, we want this portfolio to have the following payoffs (30 and 0, respectively):
\( \Delta \times S_{up} + B \times (1+R) = C_{up} = 30 \)
\( \Delta \times S_{down} + B \times (1+R) = C_{down} = 0 \)
We can solve these two equations and find:
\( \Delta = \frac{C_{up} - C_{down}}{S_{up} - S_{down}} = \frac{30-0}{150-50} = 0.3 \)
And then we can find the risk-free investment B as:
\( B =\frac{ C_{down} - \Delta \times S_{down}}{(1+R)} = \frac{0-0.3\times 50}{(1+R)} = -14.3 \)
Long story short, we have figured out that we can perfectly replicate the future payoffs of our option with the following portfolio:
- Buy 0.3 fractions of the underlying asset (S)
- Borrow 14.3 million at the risk-free rate of return.
Now why is this of any help? Because we know the value of the two assets in the replicating portfolio!
- At the current valuation S0 = 100 million. 0.3 units of the underlying asset therefore have a value of 30 million today.
- Moreover, 14.3 million of debt (B) have a value of -14.3 million.
Consequently, the present value of the replicating portfolio is 15.7 million:
Value of replicating portfolio = Δ×S0 + B = 0.3 × 100 - 14.3 = 15.7 million.
Because the option promises the exact same cash flows as the replicating portfolio, its present value must also be the same! If that were not the case, there would be an arbitrage opportunity for investors (an opportunity to make money without any risk).
Assume, for example, that the option price is only 10 million (the option is severely underpriced). What would happen?
- All investors would buy the option at 10 million and, at the same time, sell the replicating portfolio for 15.7 million. This provides them with a net cash inflow of 5.7 million today [= -10 + 15.7].
- In one year, the future payoffs the option generates (30 or 0) will exactly match the payoffs the investors have to make because they sell the replicating portfolio today. Consequently, the net cash flow in 1 year will be zero.
- The investment strategy would therefore generate a risk-free profit of 5.7 million today.
- Of course, such an arbitrage opportunity would attract a lot of investors. If everybody buys the option, the price of the option goes up. Moreover, if everybody sells the replicating portfolio, the value of the underlying asset might go down. Ultimately, the arbitrage opportunity will disappear and the option price will move to its fair value.
In contrast, if the price of the option is larger than its fair value (e.g., 20 million instead of 15.7 million), the arbitrage traders would do the opposite. They would buy the replicating portfolio and sell the option to lock-in a risk-free profit.
In the above example, we can be confident that the price of the option corresponds to its fair value because otherwise, arbitrage traders would come and exploit the opportunity. We have also seen, however, how perfect the markets must be for this arbitrage to work. To state one obvious example, we have bought (or sold) 0.3 units of the underlying asset to build the replicating portfolio. In the context of real options, however, we will hardly ever be able to observe a market price for the underlying asset, let alone will we be able to buy and sell fractions of the asset at this particular price. Therefore, investors will not be able to build suitable replicating portfolios to price the option and exploit potential misvaluations.
Similar considerations apply for the other key assumptions. When we value real options with such models, we therefore have to accept that the value estimates will be relatively imprecise and that there can be a large difference between the "value" and the "price" if arbitrage is difficult.