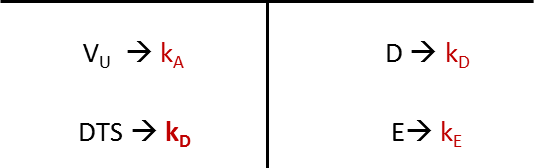Reading: The Relevance of Taxes

Let's start with a company that pursues a financing policy with a target debt level (e.g., 2'500 of debt). As we have argued before, the appropriate discount rate for the interest tax savings of such a firm is the firm's cost of debt, k_D.

The following figure summarizes the relevant costs of capital for the different sources of value of such a company:

As we know from before, the total expected return generated by the left side of the balance sheet must correspond to the total expected return that the providers of capital claim:

\( V_U \times k_A + DTS \times k_D = D \times k_D + E \times k_E \)

Solving this expression for k_A yields:

\( k_A = k_D \times \frac{D-DTS}{D-DTS+E} + k_E \times \frac{E}{D-DTS+E} \)

Solving the expression for k_E yields:

\( k_E = k_A + (k_A - k_D) \times \frac{D-DTS}{E} \) 

Let us apply these considerations to our sample firm from before. Remember that we have collected the following information about the firm under a financing policy with a constant amount of debt of 2'500:

• Cost of assets (k_A) = 12%
• Debt outstanding (D) = 2'500
• Cost of debt (k_D) = 10%
• Annual interest payments (k_D × D) = 250
• Corporate tax rate (τ) = 35%
• Annual tax savings (k_D × τ) = 87.5
• Discount rate for the DTS = k_D
• Debt tax shield (DTS) = 875
• Equity value (k_E) = 1'625.

With this information, we can estimate the firm's cost of equity under the revised financing policy:

\( k_E = k_A + (k_A - k_D) \times \frac{D-DTS}{E} = 0.12 + (0.12 - 0.10) \times \frac{2'500 - 875}{1'625} \) = 14%.

This is the same equity return as we have computed for the levered firm in a world without taxes. Remember from the firm's income statement that the expected net income is 227.5. Under our assumptions, this corrsponds to the expected annual equity cash flow. Capitalizing this cash flow perpetuity at the cost of equity of 14% does indeed yield an equity value of 1'625:

Equity value = \( \frac{\text{Equity cash flow}}{\text{Cost of equity}} = \frac{227.5}{0.14} \) = 1'625.