Reading: Understanding and Valuing Debt and Equity

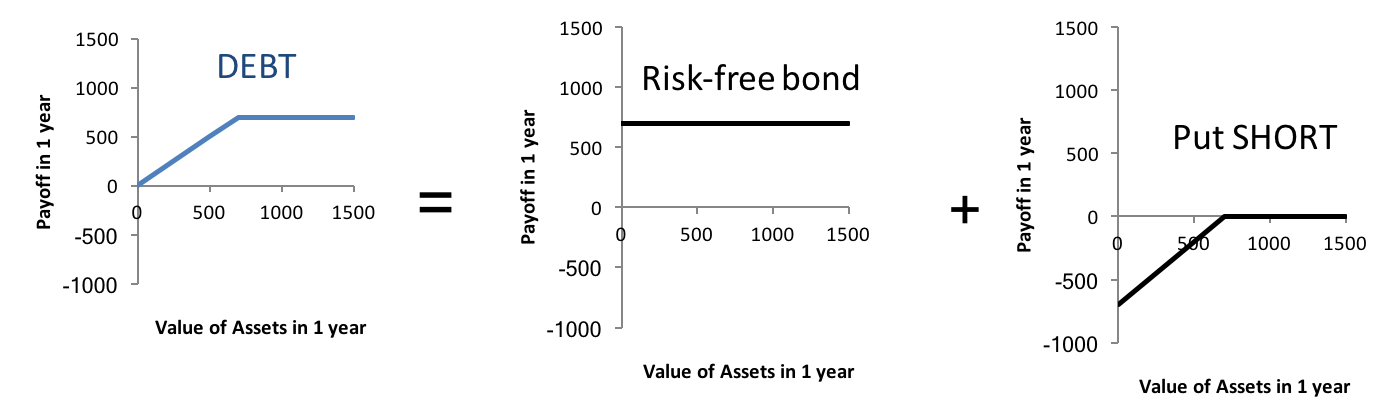
Debt

The first element of the following graph shows the payoff of the debt claim (700) at maturity from the previous page. The remaining two elements show that we can perfectly replicate the payoff of the debt claim at maturity with the following two instruments:

• A risk-free bond with a notional value of 700 and maturity 1 year
• A put option short with an exercise price equal to the notional amount of debt outstanding (700) and a time to maturity of 1 year.

 

 

Presumably, these two instruments need some additional explanations:

• Risk-free bond: A debt claim for which there is no uncertainty that it will be paid back in full and on time at maturity. Government bonds of solvent countries are usually considered "risk free." Because the bond in question is risk free, its payoff at maturity (in 1 year) is the same (namely 700 in our example), regardless of the future firm value. This is what the chart in the middle shows.
• Put option short: This one might be a bit trickier. First some terminology. 
  • Option refers to the RIGHT to conduct a transaction, not an OBLIGATION. That is, the owner of the option can choose whether or not he wants to exercise it.
  • The question is what kind of a right the option brings about. We distinguish between rights to buy (so-called CALL options) and rights to sell (so-called PUT options). In our case, we are faced with a put option, that is, a right to sell. We will get to know the call option further down when analyzing the firm's equity.
  • Then, the question is whether we own the right (a so-called LONG position) or whether we have granted that right to someone (a so-called SHORT position). 
  • A put option short, therefore, means that we have granted someone the right to sell us the assets of the firm at a predefined price (namely 700) at a predefined point in time (namely in 1 year).

  

To learn more about the basics of options, there is a fairly good tutorial on Investopedia. Moreover, our module Startup Valuation has a fairly extensive discussion about the use of option pricing models for the valuation of companies. 

 

To see that a portfolio of risk-free bond and put short perfectly replicates the payoffs of the firm's debt at maturity, consider the following table:

 

Firm value in 1 year	Debt payoff in 1 year	Replicating portfolio in 1 year
		Risk-free bond	Put short	Total
0	0	700	-700	0
500	500	700	-200	500
700	700	700	0	700
1000	700	700	0	700

 

Let's discuss these numbers in detail.

• Firm value = 0
  • If the firm is worthless at maturity (firm value of 0), the debtholders recieve no payoff.
  • In the replicating portfolio:
    • Tthe risk-free bond pays its notional amount of 700, regardless of the value of the company.
    • The put short means that the counterparty can sell us the assets of the firm (which are worthless in this scenario) at a price of 700. The counterparty will exercise this right and we have to buy the worthless assets at a price of 700. Consequenlty, we incurr a loss of 700.
    • Overall, the payoff of the replicating portfolio is therefore also 0 (+700 from the bond and -700 from the put short)

• Firm value = 500
  • The debtholders receive the full value of the firm (500)
  • In the replicating portfolio:
    • The risk-free bond pays the notional amount of 700
    • The counterparty has the right to sell us at 700 the firm's assets with a value of 500. The counterparty will exercise this right and we have to buy at 700 assets with a value of 500. We incurr a loss of 200.
    • Overall, the payoff of the replicating portfolio is therefore also 500 (+700 from the bond and - 200 from the put short)

• Firm value = 700
  • The debtholders just break even and cover their full claim of 700
  • Replicating portfolio
    • The risk-free bond still pays 700
    • The counterparty has the right to sell us at 700 the firm's assets with a value of 700. This right is worthless. If the counterparty exercises, we buy the assets at 700 and sell them in the market at the same price. The net effect is therefore 0 (assuming no transaction costs)
    • The payoff of the portfolio is therefore also 700 (700 from the bond and 0 from the put short)

• Firm value = 1'000
  • The debtholders receive their full claim of 700
  • Replicating portfolio
    • The risk-free bond still pays 700
    • The counterparty has the right to sell us at 700 the firm's assets with a value of 1'000. This right is worthless. The counterparty is better off selling the assets in the market at 1'000.  The put short will therefore not be exercised.
    • The payoff of the portfolio is therefore also 700 (700 from the bond and 0 from the put short)

  

In sum, we have managed to perfectly replicate the debt cash flows with a portfolio that consists of a risk-free bond and a put short on the firm's assets. Knowing this replicating portfolio is useful for various reasons:

• Valuation: Because the debt and the replicating portfolio have identical cash flows, they must also have identical values. Put differently, if we do not know how to value the debt directly, we can value the individual constituents of the replicating portfolio. The total value of the replicating portfolio must then correspond to the value of the firm's debt.
• Value drivers: The input factors for the valuation models of the replicating assets will give us information about what drives the value of the firm's debt.
• Credit risk analysis: We will also be able to make some useful observations about the firm's credit risk, i.e., the inability to pay its financial obligations in full and on time.

 

On the following pages, we will discuss these elements in more detail. Before doing so, let us quickly look at the firm's equity as a derivative on its assets.

 

Equity

From the previous pages, we know that the shareholders receive the residual value of the firm after all financial obligations have been satisfied:

 

 

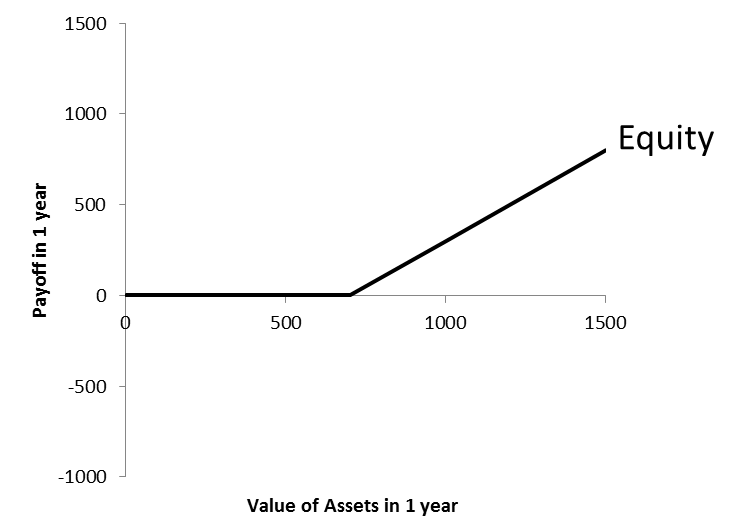
In option terminology, the shareholders own a call option (long) on the firm's assets with an excercise price equal to the notional amount of debt outstanding (700). What exactly does that mean?

• From above, we know that a call option represents a RIGHT (but not an obligation) to BUY. 
• In our specific case, the shareholders factually have the right to buy the firm's assets at a price of 700 at the time the debt matures (in 1 year). When will they exercise this right?
  • As long as the fair value of the assets is below 700 at maturity, exercising the right makes no sense. Suppose, for example, the value of the firm is 500. Exercising the right would mean that the shareholders buy at 700 something with a value of only 200. This would lead to an instantaneous loss of 200. Consequently, at maturity, the right to buy is worthless as long as the value of the firm is below the exercise price.
  • If the value of the assets exceeds the exercise price price at maturity, the right to buy becomes valuable. For example, at a firm value of 1'000, the shareholders have the right to buy the firm at a price of 700. By exercising this right, they make a gain of 300.

 

The following table summarizes the payoffs of the firm's equity as well as the replicating "portfolio" with a call long:

• In line with the descriptions above, the right to buy expires unexercised in 1 year as long as the firm value at maturity is below the exercise price of 700 (the amount of debt outstanding).
• If the firm value at maturity exceeds the amount of debt outstanding, the shareholders exercise the option, pay 700 to the debtholders and pocket the difference.

 

Firm value in 1 year	Equity payoff in 1 year	Call long payoff in 1 year
0	0	0
500	0	0
700	0	0
1000	300	300

  

Having seen how we can replicate the debt and equity payoffs with alternative financial instruments, we can now turn to the valuation of these instruments as well as the assessment of the relevant value drivers.