Reading: Understanding and Valuing Debt and Equity

• The market value of the firm’s assets (V_L) is 1’000
• The firm's debt outstanding has a notional value of 500 (zero-coupon bond)
• This notional value will be paid at maturity in 3 years
• The risk-free rate of return is 1% (discrete compounding)
• The volatility of the firm’s asset return is 30%.

• The value of the firm’s debt (D) and equity (E)
• The yield to maturity of the firm’s debt as well as its credit spread
• The implied probability of default
• The present value of the expected credit loss
• The expected loss in default.

Equity Valuation

Let's start with the valuation of the firm's equity. From the previous page, we know that the equity is equivalent to a call option on the firm's assets with an exercise price that is equal to the notional amount of debt outstanding. The company description above provides us with the necessary information to map the model parameters:

• Current value of the underlying asset (V): 1'000
• Exercise price: 500
• Time to maturity: 3 years
• Risk-free rate of return: 1%
• Volatility of the firm's assets: 30%

When we plug these parameters in the valuation model from the previous page, we obtain:

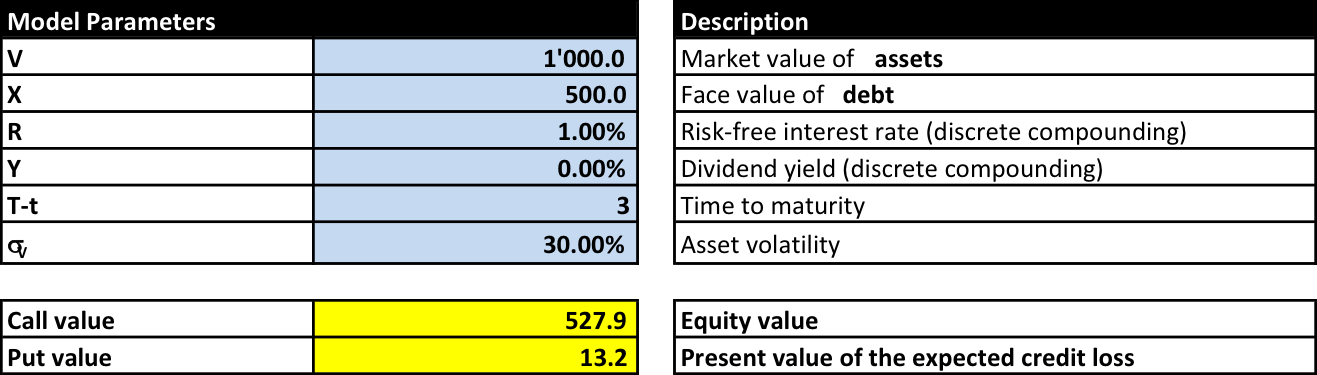
According to the model estimates, a call option with these characteristics therefore has a value of 527.9. This is the value of the firm's equity (E), according to the model.

Debt Valuation

To value the firm's debt, we can proceed in two ways. The easiest is to remember that the overall value of the firm corresponds to the value of debt and equity: V_L = D + E. Consequently,

D = V_L - E = 1'000 - 527.9 = 472.1.

Alternatively, we can look at debt as a risk-free bond plus a put short on the firm's assets:

• Value risk-free bond =  \( \frac{B}{(1+R)^{T-t}} = \frac{500}{1.01^3} \) = 485.3
• Value of a put short = -13.2, according to the model output above.

Consequently:

D = Value risk-free bond - Put short = 485.3 - 13.2 = 472.1.

Both approaches yield a debt value (as of today) of 472.1.

Yield-to-Maturity and Credit Spread of Corporate Debt

Next, we can assess the yield-to-maturity (YTM) as well as the credit spread of the firm's debt. The yield to maturity indicates the rate of return the bond in question promises the investors if they buy it today and hold it until maturity. In our example, the current value of the bond is 472.1 and the promised payment at maturity in 3 years is 500.

\( D = \frac{\text{Notional value}}{(1+YTM)^{T-t}} \)

The zero-bond's YTM, therefore, is:

\( YTM = (\frac{\text{Notional value}}{D})^{\frac{1}{T-t}} -1 \)

\( YTM = (\frac{500}{472.1})^{\frac{1}{3}} - 1 \) = 1.93%.

Put differently, if the debtholders buy the bond today and hold it until maturity, the bond promises them an annual return of 1.93%.

With this information, we can now also compute the bond's credit spread. The credit spread indicates the risk premium that a bond has to pay on top of the risk-free rate of return to compensate the investors for the bond's credit risk (i.e., the fact that the bond is not risk free):

Credit spread = YTM - Risk-free rate of return = 1.93% - 1.00% = 0.93%.

The bond's credit spread is 0.93% or 93 basis points.

Expected Credit Loss

Another way to assess the firm's credit risk is to look at value implications of that risk. We can compare the actual value of the bond with the theoretical value of an otherwise identical risk-free bond. The value difference between the two bonds indicates the discount that market participants apply because of the firm's credit risk. This is the so-called expected credit loss:

Expected Credit Loss = D_{Risk free} - D_Actual.

We know the two values from our debt valuation above:

• The actual value of the firm's debt is 472.1
• The value of an otherwise identical risk-free bond is 485.3

Hence, the present value of the expected credit loss is 13.2:

Expected credit loss = D_{Risk free} - D_Actual = 485.3 - 472.1 = 13.2.

Alternatively, we have seen that the bond's replicating portfolio consists of a risk free bond and a put option short. The value of the put option short must therefore correspond to the expected credit loss. This is exactly what the model tells us.

Market participants discount the current value of the bond by 13.2 (dollars, francs, etc.) because of the associated credit risk. If the firm became riskier, this discount would increase. In contrast, if it disposed of some of its risks, the discount would drop.

Default Probability and Expected Loss in Default

The last two important pieces of information that we can extract from the model are the firm's default probability as well as the expected loss in default. The default probability indicates the likelihood that the firm will will not be able to make the contractual debt payments in full and on time. The loss in default, in turn, tells us how much the debtholders stand to lose in the event that the bond actually defaults. Together, the default probability and the loss in default determine the expected credit loss that we have computed above:

Expected credit loss = Default probability × Expected loss in default

For example, if a bond has a 10% default probability and the debtholders expect to lose 100 (in present value) in the case the bond defaults, the expected credit loss is 10: With probability 10% they lose 100, with probability 90% the bond does not default and they lose nothing.

In our case above, the expected credit loss was 13.20. But what about the default probability and the expected loss in default?

The firm defaults on its debt if, at maturity, the asset value drop below the notional amount of debt outstanding:

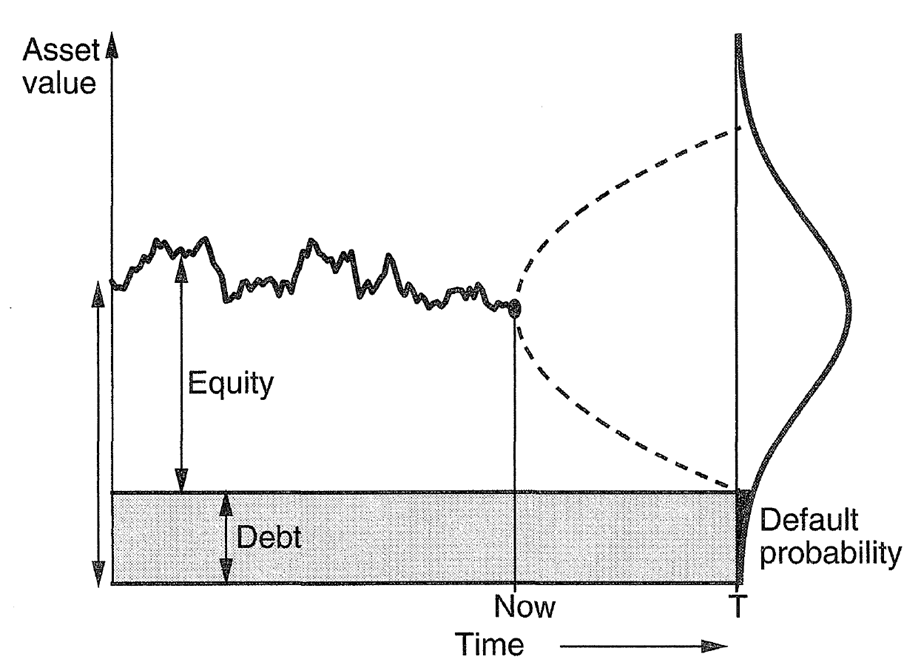
If the firm does not default on its debt at maturity, the asset value exceeds the notional amount of debt and the shareholders exercise their call option to buy the firm at an exercise price equal to the notional amount of debt. In other words, the probability that the shareholders do not exercise their call option corresponds to the firm's default probability. 

It can be shown that in the option pricing model from before, the parameter N(-d₂) captures that probability (i.e., the probability that a standard normal variable does not exceed -d₂.

Probability of default = N(-d₂) = 12.89%.

Conditional on the model assumption, the current company valuation implies that the market participants expect the firm to default on its debt with a probability of roughly 13%. With this information at hand, we can now also compute the expected loss in default. To do so, we solve the above equation for the expected loss in default:

Expected loss in default = \( \frac{\text{Expected credit loss}}{\text{Default probability}} \)

Consequently, the firm's expected credit loss is 102.5:

Expected credit loss = \( \frac{13.2}{0.1289} \) = 102.5.

If the firm defaults, debtholders therefore expect to incurr a loss of 102.5, on average (in present value). 

Summary

This example has illustrated the rich set of information that we can extract from the Merton model. 

• First, we have used the model to decompose the value of the firm into its components equity value and debt value, using option pricing.
• Second, we have also used the model to better understand the firm's credit risk. To this end, we have computed:
  • the annual return the bond promises to pay to the debtholders (the yield-to-maturity)
  • the premium the bond promises to pay on top of the risk-free rate of return (the credit spread)
  • the implied default probability of the firm
  • the expected loss in the case the firm actually defaults (the expected loss in default)
  • and the expected value of the loss in default (the expected credit loss).

When using the model, it is important to understand that it relies on a set of rather restrictive assumptions, many of which we discuss in more detail in the respective section of the module Startup valuation. Because these assumptions are rarely met in practice, we have to accept that the model output can only be used as rough estimates of the relevant parameters. While the absolute values of the model might therefore not always be very meaningful, the Merton model helps us understand how and why the firm's valuation and credit risk change if its key characteristics change. Therefore, the comparative statics of the model would seem to be rather useful in many situations. We will consider some of them in the next section, also to practice the model a bit more.