Reading: Understanding and Valuing Debt and Equity

Now that we have seen the Merton model at work, let's look at a few additional examples to revisit the key determinants of the value of debt and the firm's credit risk.

Extension 1: Asset substitution problem

Consider the same firm as in the previous example. Now let us assume that the shareholders come across a project that has a net present value of -20 (it destroys value) but doubles the volatility of the firm's assets from 30% to 60%. Will the shareholders take the project?

The following figure shows the revised analysis. Compared to the previous situation, what changed is that the overall value of the firm drops by 20 to 980 because of the new project and the volatility of the firm's assets increases from 30% to 60%.

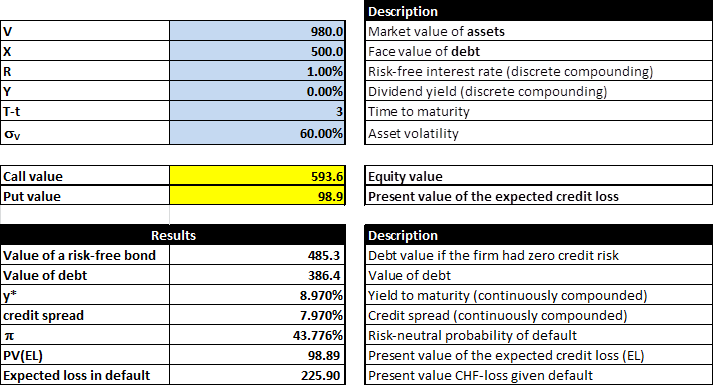
What are the net effects of the new project?

• We see that the value of the firm's equity (call long) increases to 593.6 (from 527.9). Depsite the fact that the overall value of the project is negative, shareholders gain 65.7 [= 593.6 - 527.9] from taking it. The reason is that the additional risk of the firm gives the firm more upside potential, which, as we have seen, goes to the shareholders. It also gives the firm a higher downside risk, which the shareholders share with the debtholders.
• The ones who suffer from the project are the debtholders. Their claim drops in value from 472.1 to 386.4. This drop by 85.7 has two reasons:
  • First, the project destroys a firm value of 20
  • Second, the shareholders redistribute 65.7 of wealth from the debtholders into their own pockets. 
• The wealth redistribution of 65.7 is the result of the firm's higher credit risk with the project. The model output above shows that the probability of default increases to almost 44% (up from roughly 14%) with the new project. 

If the debt covenants do not prevent such actions, the shareholders might have a financial incentive to pursue such risk-increasing but value-destroying projects.

Extension 2: Additional borrowing

Now suppose the firm wants to issue additional debt with a notional amount of 700 to conduct a project that will increase the overall value of the firm by 800 to 1'800. The riskiness of the firm and the maturity of the debt claims remain the same. However, the new debtholders insist that their claim will be senior to the one of the original debtholders. How does this affect the analysis?

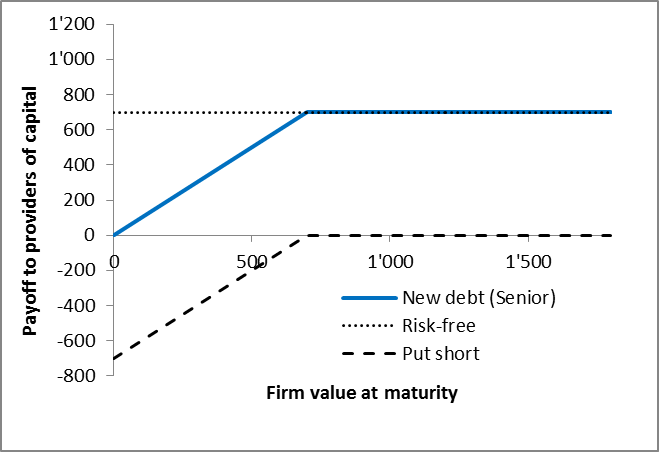
The following figure shows how the various claimholders will split the value of the firm at maturity in 3 years. The key takeaways are as follows:

• Because the claim of the new debtholders is senior to the one of the original debtholders, the new debtholders have absolute liquidation preference. This means that they will be the first to receive their notional amount. Consequenlty, the first 700 in firm value will go to the new debtholders, as shown by the blue line in the figure below.
• The claim of the original debtholders is junior to the new debt but senior to the equity. Consequenlty, they start receiving a payoff as soon as the value of the firm at maturity exceeds the 700 that go to the new debtholders. Since the notional amount of the original debt is 500, the original debtholders will receive their maximum compensation at a firm value of 1,200. This is what the green line depicts in the figure below.
• The shareholders' claim is junior. They only receive a compensation after all the debt claims have been satisfied. As we have seen before, this is the case at a firm value that exceeds 1'200, i.e., the total amount of debt outstanding. Thereafter, all the value-added goes to the shareholders, as shown by the red line in the figure below.

As in the case with a single source of debt, we can build replicating portfolios for the various financial claims. To do so, we follow the same logic as before. 

• The new senior debt is logically equivalent to the senior debt in the original example: 
  • Risk-free bond with a notional value of 700, i.e., the notional amount of the firm's new debt
  • A put option short with an exercise price equal to the notional amount of senior debt (700)
     

• The replicating portfolio of the original (now "subordinated" or "junior") debt is a bit trickier:
  • Under the new financing structure, the original debtholders start participating in firm value as soon as the value exceeds 700, i.e, the notional amount of the senior debt. Consequently, the subordinated debt is equivalent to a call option long on the firm's assets with an exercise price equal to the notional amount of senior debt (700). As
  • As we have seen, the junior debt reaches its maximum payoff at a firm value of 1'200 (the total amount of debt outstanding). Thereafter, the shareholders take over. At a firm value of 1'200, the original debtholders therefore give away the additional proceeds of the firm. This is equivalent to a call option short on the firm's assets with an exercise price equal to the total amount of debt outstanding.
     

• The firm's equity remains logically the same: A call option on the firm's assets with an exercise price equal to the total amount of debt outstanding, namely 500 + 700 = 1'200.
   

Following this logic, we can now value the replicating portfolios using the option pricing model from before. 

New debt (senior):

• Risk-free bond with a notional value of 700:
   
  Value of risk-free bond = \( \frac{700}{1.01^3} \) = 679.4
   
• Put option short with an exercise price of 700. According to the model output below, the value of such a put short is -6.6:
   
  
   
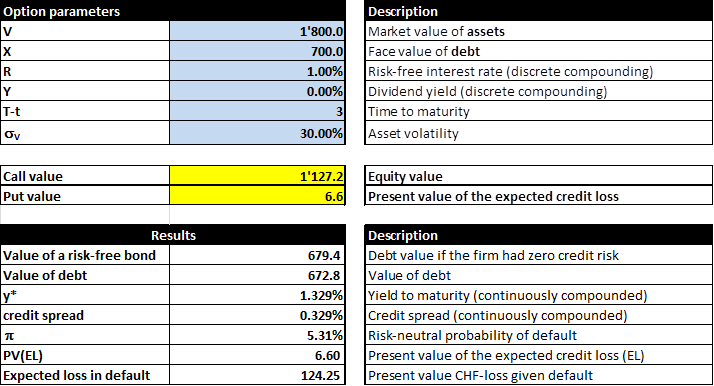
• The value of the new senior bond, therefore, is 679.4 - 6.6 = 672.8

Original debt (subordinated)

• Call option long with an exercise price of 700. According to the figure above, the value of that call option is 1'127.2.
• Call option short with an exercise price of 1'200. According to the model output below, the value of such a call short is -718.2:
   
   
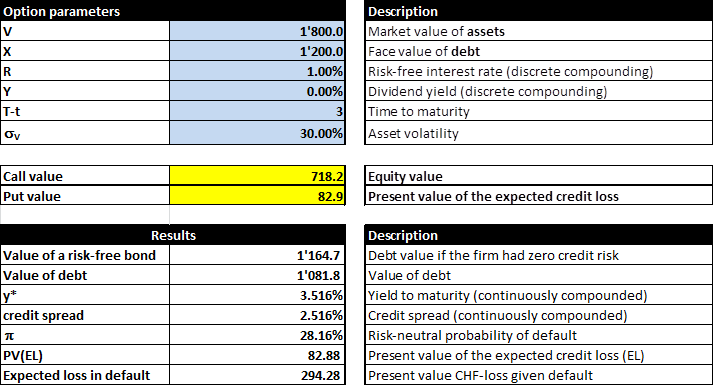
• The value of the original debt will therefore be 1'127.2 - 718.2 = 409.0 after the additional round of financing.

Equity:

• Call option with an exercise price of 1'200.
• According to the above model output, the value of such a call option is 718.2. Consequently, this is the equity value after the new (debt financed) project.

Discussion:

• This example has shown how to extend the Merton model to a firm with senior and junior debt outstanding.
• The new element was the valuation and analysis of the firm's junior debt.
  • We have seen that junior debt factually combines the characteristics of equity and senior debt. 
  • Junior debtholders "feel" like shareholders if the firm value is low compared to the debt outstanding. In this case, they have a convex claim and therefore a preference for more risk.
  • In contrast, they "feel" like ordinary debt holders if the firm value is high compared to the amount of debt outstanding. In this case, they have a concave claim and are therefore risk averse.
• In our particular case, the firm issued new senior debt, which moved the original debt to a junior position. This refinancing of the company is not in the best interest of the original debt holders:
  • While the equity value increases (from 527.9 to 718.2), the value of the original debt drops from 472.1 to 409.0. Even though the firm pursues a project with a positive net present value (NPV) the original debtholders lose money!
  • The reason is that the financing of the new project moves the original debtholders down in the liquidation preference, which increases their credit risk.
• Given these results, it is not surprising that debt covenants generally prevent firms from issuing debt claims with the same or better seniority.