Reading: Future Value
2. A Simple Example
Let us start with a simple example: Suppose you can invest $1'000 today in an investment opportunity that generates a return of 10% per year. This interest is paid once at the end of the year. How much money will you have in 1 year?
This simple question has an equally simple answer: $1'100. On your investment of $1'000 you earn a return of 10% or 0.1 × $1'000 = $100. In one year, you will therefore have the invested capital of $1'000 plus the investment return of $100, for a total future value of $1'100.
More formally, let us use the following notation:
| Variable | Description | Value in Example |
| C0 | Cash flow today | $1'000 |
| R | Annual rate of return | 10% |
| T | Investment horizon (number of years) | 1 |
| FV | Future Value of Investment | 1'100 |
To solve the simple investment problem from before, we can write:
\( FV_1 = C_0 + C_0 \times R = C_0 \times (1+R) = 1'000 \times 1.1 = 1'100.00 \)
How much money will the investment generate if we extend the investment horizon from 1 year to 2 years (at the same annual rate of return and without withdrawing any money after 1 year)?
During the second year of the investment, we put the initial capital of $1'000 as well as the first year's return of $100 to work. Consequently, in the second year, we earn interest on the invested capital as well as on the interest from the first year. The total interest payment for year 2 is 0.1 × 1'100 = $110, so that after two years, the future value of the investment is $1'210:
\( FV_2 = FV_1 \times (1+R) = 1'100 \times 1.1 = 1'210 \)
If we plug the first equation into the second one, we can write:
\( FV_2 = FV_1 \times (1+R) \)
\( FV_2 = C_0 \times (1+R) \times (1+R) \)
\( FV_2 = C_0 \times (1+R)^2 = 1'000 \times 1.1^2 = 1'210. \)
More generally speaking, if we invest an amount C at time t (t= 0 if the investment is today) at a rate of return of R until time T, the future value at the end of period T will be:
\( \bf{FV_T = C_t \times (1+R)^{(T-t)}} \)
We can use this equation to compute the future values of our investment after, say, 3, 4, and 5 years, respectively:
\( FV_3 = C_0 \times (1+R)^3 = 1'000 \times 1.1^3 = 1'331 \)
\( FV_4 = C_0 \times (1+R)^4 = 1'000 \times 1.1^4 = 1'464.1 \)
\( FV_5 = C_0 \times (1+R)^5 = 1'000 \times 1.1^5 = 1'610.51 \)
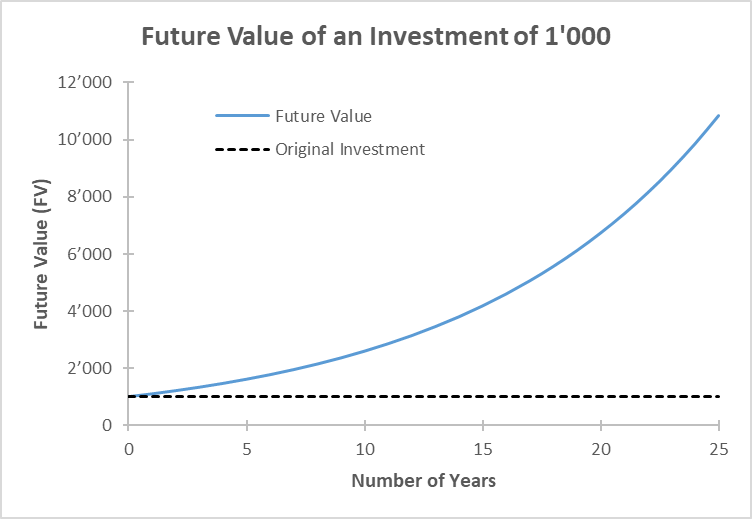
The blue line in the following graph shows the future value of the investment as a function of the investment horizon (T years). As a comparison, the dashed black line depicts the original investment of $1'000:
The graph offers some important takeaways:
- First, it confirms that $1'000 today are more valuable than $1'000 in, say, 5 years. If we have the money today, we can invest it and collect total interest payments of $610.51, according to our computations above. We forego these interest payments if we only receive the $1'000 in 5 years.
- The future value of the investment does not grow linearly, but exponentially. The reason is that, after the first year, we earn interest not only on the invested capital but also on the accumulated interest payments since the beginning of the investment. This is the so-called Compound Interest (or Interest on Interest).
- In our computations above, we have already seen compound interest at work:
- For the first year, the dollar return of the investment is $100 [= 1'000 × 0.1].
- For the second year, the dollar return is $110 [= (1'000 + 100) × 0.1].
- For the third year, the dollar return is $121 [= (1'000 + 100 + 110) × 0.1].
- When we fast-forward to the 25th year, it could be shown that the investment would earn a dollar return of $985 for that year.
- And when we fast-forward to the 100th year, it could be shown that that year's dollar return would be more than $1.25 MILLION!
This clearly confirms the popular wisdom from the introductory remarks. The more time money has to grow, the quicker it will grow (at a given rate of return). Eventually, the interest payments will dwarf the original capital.