Lektüre: Zukunfstwerte (Future Values)
2. Ein einfaches Beispiel
Beginnen wir mit einem einfachen Beispiel: Angenommen, Sie können heute 1'000 Dollar in eine Anlagemöglichkeit investieren, die eine Rendite von 10% pro Jahr abwirft. Diese Zinsen werden einmal am Ende des Jahres ausgezahlt. Wie viel Geld werden Sie in einem Jahr haben?
Auf diese einfache Frage gibt es eine ebenso einfache Antwort: 1'100 Dollar. Auf der Investition von 1'000 Dollar erhalten Sie eine Rendite von 10% oder 0.1 × 1'000 = 100 Dollar. In einem Jahr verfügen Sie also über das investierte Kapital von 1'000 Dollar zuzüglich der Investitionsrendite von 100 Dollar, also über einen zukünftigen Gesamtwert (Zukunfstwert, Future Value) von 1'100 Dollar.
Um diese Beziehung zu formalisieren, verwenden wir die folgende Notation:
| Variable | Beschrieb | Wert im Beispiel |
| C0 | Cashflow (C) heute | 1'000 Dollar |
| R | jährliche Rendite | 10% |
| T | Investitionshorizont (Anzahl Jahre) | 1 |
| FV | Zukunfstwert (Future Value) der Investition | 1'100 Dollar |
Um das einfache Investitionsvorhaben von vorhin zu lösen, können wir schreiben:
\( FV_1 = C_0 + C_0 \times R = C_0 \times (1+R) = 1'000 \times 1.1 = 1'100.00 \)
Wie viel Geld wird die gleiche Investition einbringen, wenn wir den Anlagehorizont von 1 Jahr auf 2 Jahre verlängern (bei gleicher jährlicher Rendite und ohne Geldentnahme nach 1 Jahr)?
Im zweiten Jahr der Investition setzen wir zusätzlich zum Anfangskapital von 1'000 Dollar auch die im ersten Jahr erwirtschaftete Rendite von 100 Dollar ein. Folglich erhalten wir im zweiten Jahr Zinsen auf das investierte Kapital sowie auf die Zinsen aus dem ersten Jahr (sog. Zinseszinsen). Die gesamte Zinszahlung für das Jahr 2 beträgt demnach 0.1 × 1'100 = 110 Dollar, so dass der zukünftige Wert der Investition nach zwei Jahren 1'210 Dollar beträgt:
\( FV_2 = FV_1 \times (1+R) = 1'100 \times 1.1 = 1'210 \)
Wenn wir die erste Gleichung in die zweite einsetzen, können wir schreiben:
\( FV_2 = FV_1 \times (1+R) \)
\( FV_2 = C_0 \times (1+R) \times (1+R) \)
\( FV_2 = C_0 \times (1+R)^2 = 1'000 \times 1.1^2 = 1'210. \)
Allgemeiner ausgedrückt: Wenn wir zum Zeitpunkt t (t= 0 wenn die Investition heute erfolgt) den Betrag C mit einer Rendite von R investieren und bis zum Zeitpunkt T halten, ist der zukünftige Wert (Future Value, FV) am Ende der Periode T gleich:
\( \bf{FV_T = C_t \times (1+R)^{(T-t)}} \)
Mit dieser Gleichung können wir den Zukunfstwert unserer Investition nach beliebig vielen Jahren berechnen. Zum Beispiel:
\( FV_3 = C_0 \times (1+R)^3 = 1'000 \times 1.1^3 = 1'331 \)
\( FV_4 = C_0 \times (1+R)^4 = 1'000 \times 1.1^4 = 1'464.1 \)
\( FV_5 = C_0 \times (1+R)^5 = 1'000 \times 1.1^5 = 1'610.51 \)
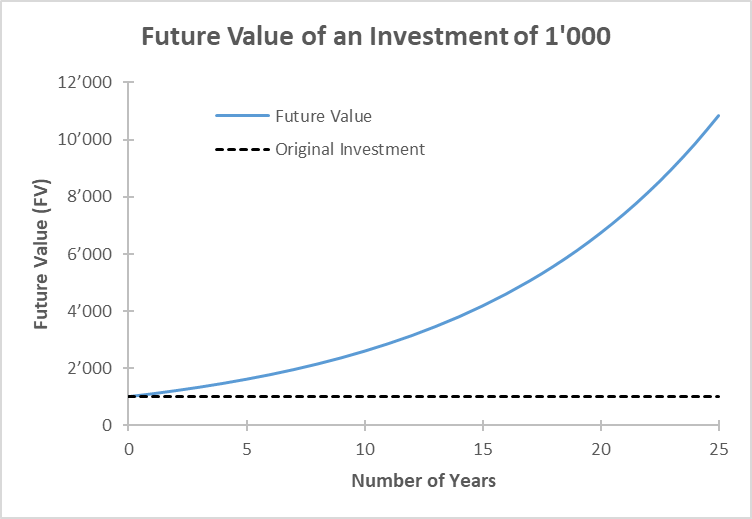
Die blaue Linie in der folgenden Grafik zeigt den zukünftigen Wert der Investition in Abhängigkeit vom Anlagehorizont (T Jahre). Zum Vergleich zeigt die gestrichelte schwarze Linie die ursprüngliche Investition von 1'000 Dollar:
Die Abbildung liefert einige wichtige Erkenntnisse
- Erstens bestätigt sie, dass 1'000 Dollar heute mehr wert sind als 1'000 Dollar in beispielsweise 5 Jahren. Wenn wir das Geld heute haben, können wir es investieren und gemäss unseren obigen Berechnungen Zinszahlungen von insgesamt 610.51 Dollar erhalten. Wir verzichten auf diese Zinszahlungen, wenn wir die 1'000 Dollar erst in 5 Jahren erhalten.
- Der zukünftige Wert der Investition wächst nicht linear, sondern exponentiell. Der Grund dafür ist, dass wir nach dem ersten Jahr nicht nur Zinsen auf das investierte Kapital erhalten, sondern auch auf die seit Beginn der Investition aufgelaufenen Zinszahlungen. Dies ist der so genannte Zinseszins-Effekt.
- In unseren obigen Berechnungen haben wir bereits gesehen, wie der Zinseszins wirkt:
- Im ersten Anlagejahr betragen die Zinseinnahmen auf der Investition 100 Dollar [= 1'000 × 0.1].
- Im zweiten Anlagejahr liegen die Zinsen bei 110 Dollar [= (1'000 + 100) × 0.1].
- Im dritten Anlagejahr betragen die Zinsen 121 Dollar [= (1'000 + 100 + 110) × 0.1].
- Wenn wir zum 25. Anlagejahr vorspulen, könnte gezeigt werden, dass die Investition in diesem Jahr Zinszahlungen von 985 Dollar einbringen würde.
- Der gleichen Logik folgend würden die Zinszahlungen im 100. Anlagejahr mehr 1.25 MILLIONEN Dollar betragen!
Dies bestätigt eindeutig die Volksweisheit aus den einleitenden Bemerkungen. Je mehr Zeit das Geld zum Wachsen hat, desto schneller wächst es (bei einer bestimmten Rendite). Irgendwann werden die Zinszahlungen das ursprüngliche Kapital in den Schatten stellen.