4. Readings: Future Values with Multiple Cash Flows

In the preceding section, we have seen that the principle of value additivity allows us to compute the future value of a string of cash inflows as the sum of the future value of each individual cash inflow. 

This section shows that the principle of value additivity is not limited to cash inflows, but applies to any cash flow string.

Example 3

Suppose you invest 20'000 today in a bank account that earns an annual return of 4%. In 2 years, you withdraw 10'000, and in 4 years, you invest another 20'000. How much money can you expect to have in the bank account in 8 years?

As before, we can compute the future value of the investment proposal using 2 ways, namely:

• Model the year-to-year development of the account balance
• Compute the sum of the future value of each individual cash flow

Modelling the Account Balance

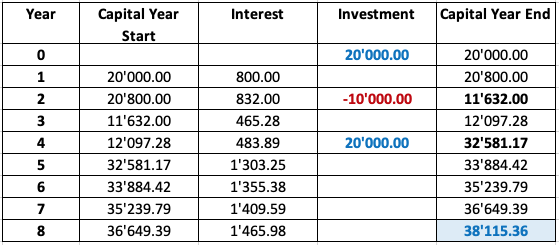
The following table shows the development of an account that earns a return of 4% and experiences the cash flows described above. See also the accompanying excel file.

In words:

• During the first 2 years, the investment of 20'000 earns an annual return of 4% (that is, 800 in year 1 and 832 in year 2), so that the balance increases to 21'632 by the end of year 2 (right before the withdrawal).
   
• At that time, you withdraw 10'000 from the account, so that there is a remaining balance of 11'632 at the end of year 2.
    
• This balance then earns interest in years 3 (11'632 × 0.04 = 465.28) and year 4 (12'097.28 × 0.04 = 483.89), so that the balance increases to 12'581.17 by the end of year 4 (right before the additional investment).
   
• With the additional investment in year 4, the total balance then increases to 32'581.17.
  
  
• On this amount, you earn interest for the remaining 4 years, so that the overall balance of the account will be 38'115.36 in 8 years.

Put differently, the procedure to obtain the future value of the account is identical to Example 1 before. The only numerical difference is that we use negative numbers for withdrawals, so that we subtract any cash outflows from the account balance at the time of the outflow.

Sum of Future Values

Alternatively, we can apply the principle of value additivity and calculated the sum of the future value of each individual cash flow to obtain the account balance in 8 years. In our standard equation from the preceding section, the only notable difference is that we use negative values for cash outflows:

\( \bf{FV_T = \sum_{t=0}^{T} C_t \times (1+R)^{(T-t)}} \)

In our example, with an initial inflow of 20'000 (C₀ = 20'000), an outflow of 10'000 in year 2 (C₂ = -10'000), and an inflow of 20'000 in year 4 (C₄ = 20'000), the future value at the end of year 8 (FV₈) is 38'115.36:

\( FV_8 = 20'000 \times 1.04^8 - 10'000 \times 1.04^6 + 20'000 \times 1.04^4 \)

\( FV_8 = 27'371.38 - 12'653.19 + 23'397.17 = 38'115.36\)

With this knowledge, we are now able to compute the future value of any cash flow stream!