4. Lektüre: Future Values mit mehreren Cashflows
5. Übungsbeispiel
Lassen Sie uns dies an einem weiteren Beispiel üben:
Beispiel 4
Nehmen wir an, dass eine Anlage die folgenden Cashflows aufweist:
- Investition von 5'000 in 1 Jahr (C1 = 5'000)
- Investition von 20'000 in 3 Jahren (C3 = 20'000)
- Ausschüttung von 8'000 in 5 Jahren (C5 = -8'000)
Wie viel Geld wird in 7 Jahren auf dem Bankkonto sein, wenn der Zinssatz 10% beträgt?
Unserem Standardverfahren folgend, können wir schreiben:
\( FV_T = \sum_{t=0}^{T} C_t \times (1+R)^{(T-t)} \)
Wenn wir den Ausdruck mit den Cashflows von oben ausschreiben, erhalten wir:
\( FV_{7} = C_1 \times (1+R)^{(7-1)} + C_3 \times (1+R)^{(7-3)} + C_5 \times (1+R)^{(7-5)} \)
\( FV_7 = 5'000 \times 1.1^6 + 20'000 \times 1.1^4 - 8'000 \times 1.1^2 \)
\( FV_7 = 8'857.78 + 29'282.0 - 9'680.0 = 28'459.8 \)
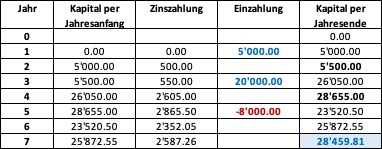
Der zukünftige Wert des Investitionsvorschlags in 7 Jahren beträgt also 28'459.8. Das gleiche Ergebnis erhalten wir, wenn wir den Saldo des Investitionskontos von Jahr zu Jahr modellieren: