Reading: Perpetuities
2. Perpetuity Due
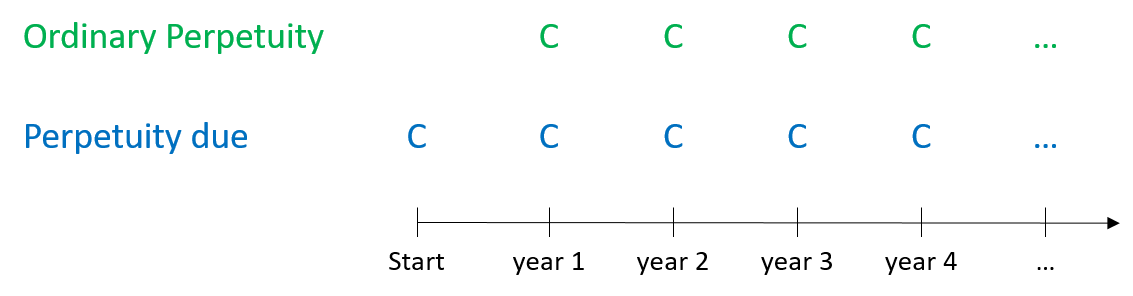
In the perpetuities that we have considered so far, we have assumed that the cash flows occur at the end of each period. More specifically, we have assumed that a perpetuity starts today, but then it takes one year for the first cash flow to arrive. Clearly, that need not necessarily be the case. It could well be that a perpetuity generates cash flows at the beginning of each investment period, so that the first payment occurs at the time the perpetuity starts.
A perpetuity that make recurring payments at the beginning of each investment period is called Perpetuity Due, whereas a perpetuity with payments at the end of each investment period is generally referred to as an "Ordinary" Perpetuity.
It's easy to see that the two types of perpetuities only differ with respect to the first cash flow. The perpetuity due makes a payment at the time it starts, the ordinary perpetuity doesn't. Thereafter, they are identical:
Consequently, adjusting the valuation formula for a perpetuity due is rather straightforward: The perpetuity due corresponds to an ordinary perpetuity, plus an initial payment of C. Since this initial payment occurs at the start of the perpetuity, it already reflects a present value and needs no further discounting. Put differently:
\( \bf{PV_{0,\text{Perpetuity Due}} = C + PV_{0, \text{Ordinary Perpetuity}}} \)
\( \bf{PV_{0,\text{Perpetuity Due}} = C + \frac{C}{R}} \)
Example 2
You have won a lottery that offers a perpetual annual payment of 200'000, starting today. The relevant discount rate is 10%. Based on this information, what is the present value of the lottery?
Since the payments start today, we are dealing with a perpetuity due. Consequently:
\( PV_{0,\text{Perpetuity Due}} = C + \frac{C}{R} = 200'000 + \frac{200'000}{0.1}=2'200'000 \)
Example 3
You can choose between the following payout schemes. All three are subject to a cost of capital of 10%:
- Alternative A: A cash payment of 2.1 million today
- Alternative B: A cash payment of 205'000 each year forever, starting in one year
- Alternative C: A cash payment of 200'000 each year forever, starting today.
To decide among the three alternatives, we need to compare their present values. The present value of alternative A is straightforward, since it is a cash payment today:
\( PV_A = 2.1 \ \text{million} \)
Alternative B is an ordinary perpetuity whereas alternative C is a perpetuity due. Consequently:
\( PV_B = \frac{C_B}{R} = \frac{205'000}{0.1} = 2.05 \ \text{million} \)
\( PV_C = C_C + \frac{C_C}{R} = 200'000 + \frac{200'000}{0.1} = 2.20 \ \text{million} \)
Based on these valuations, we should therefore opt for Alternative C (the perpetuity due), since it offers the greatest present value.