Lektüre: Ewige Renten
2. Vorschüssige Ewige Renten
Bei den bisher betrachteten nachschüssigen ewigen Renten haben wir angenommen, dass die Cashflows am Ende jeder Periode eintreten. Genauer gesagt haben wir angenommen, dass eine ewige Rente heute beginnt, es aber ein Jahr dauert, bis der erste Cashflow eintritt. Das muss natürlich nicht unbedingt der Fall sein. Es könnte durchaus sein, dass eine ewige Rente bereits zu Beginn jeder Investitionsperiode Cashflows generiert, so dass die erste Zahlung zum Zeitpunkt des Beginns der ewigen Rente erfolgt.
Eine ewige Rente, die zu Beginn jeder Investitionsperiode wiederkehrende Zahlungen leistet, wird als vorschüssige ewige Rente (engl.: Perpetuity Due) bezeichnet, während eine ewige Rente mit Zahlungen am Ende jeder Investitionsperiode allgemein als "gewöhnliche" ewige Rente oder nachschüssige ewige Rente bezeichnet wird.
Es ist leicht zu erkennen, dass sich die beiden Arten der ewigen Rente nur in Bezug auf den ersten Zahlungsstrom unterscheiden. Bei der vorschüssigen ewigen Rente wird zu Beginn eine Zahlung geleistet, bei der nachschüssigen ewigen Rente findet diese Zahlung nicht. Danach sind beide ewigen Renten identisch identisch:
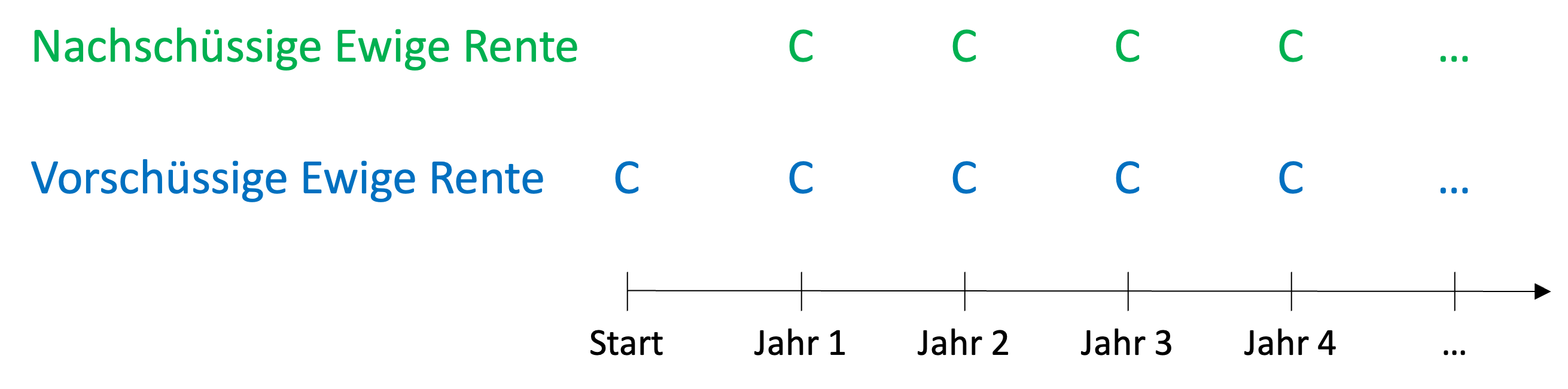
Daher ist die Anpassung der Bewertungsformel für eine vorschüssige ewige Rente recht einfach: Die vorschüssige ewige Rente entspricht einer nachschüssigen ewigen Rente zuzüglich einer Anfangszahlung von C. Da diese Anfangszahlung zu Beginn der ewigen Rente erfolgt, muss nicht weiter abgezinst werden. Anders ausgedrückt:
\( \bf{PV_{0,\text{Vorschüssige Ewige Rente}} = C + PV_{0, \text{Nachschüssige Ewige Rente}}} \)
\( \bf{PV_{0,\text{Vorschüssige Ewige Rente}} = C + \frac{C}{R}} \)
Beispiel 2
Sie haben in einer Lotterie gewonnen, die Ihnen eine konstante jährliche Zahlung von 200'000 bietet, die bereits heute beginnt. Der relevante Kapitalkostensatz beträgt 10%. Wie hoch ist der Present Value der Lotterie basierend auf diesen Informationen?
Da die Zahlungen heute beginnen, handelt es sich um eine vorschüssige ewige Rente. Folglich:
\( PV_{0,\text{Vorschüssige Ewige Rente}} = C + \frac{C}{R} = 200'000 + \frac{200'000}{0.1}=2'200'000 \)
Beispiel 3
Sie können zwischen den folgenden drei Auszahlungsmodellen wählen. Für alle drei gilt ein Kapitalkostensatz von 10%:
- Alternative A: Eine einmalige Zahlung von 2.1 Millionen heute
- Alternative B: Eine konstante jährliche Zahlung von 205'000, wobei die erste Zahlung exakt in 1 Jahr eintrifft
- Alternative C: Eine konstante jährliche Zahlung von 200'000, wobei die erste Zahlung bereits heute eintrifft
Um eine Entscheidung zwischen den drei Alternativen zu treffen, müssen wir ihre Present Values vergleichen. Der Present Value von Alternative A ist einfach, da es sich um eine Barzahlung heute handelt:
\( PV_A = 2.1 \ \text{Mio.} \)
Bei Alternative B handelt es sich um eine nachschüssige ewige Rente während Alternative C eine vorschüssige ewige Rente ist. Folglich gilt:
\( PV_B = \frac{C_B}{R} = \frac{205'000}{0.1} = 2.05 \ \text{Mio.} \)
\( PV_C = C_C + \frac{C_C}{R} = 200'000 + \frac{200'000}{0.1} = 2.20 \ \text{Mio.} \)
Auf der Grundlage dieser Bewertungen sollten wir uns daher für Alternative C (die vorschüssige ewige Rente) entscheiden, da sie den größten Present Value bietet.