Reading: Annuities

Example 3

Consider a project that requires an annual investment of 250. These capital requirements last for 5 years and are due at the beginning of each year, starting today. The discount rate is 6%. Based on this information, what's the present value of the total required investment?

In this example we are dealing with an annuity with payouts at the beginning of each investment period, a so-called annuity due. With the knowledge that we have gained so far, there are various ways to value such annuities.

Annuity Due: Cash Flow Today Plus Ordinary Annuity for T-1 years

The following figure maps the five cash flows of the project that occur at the beginning of each investment period. It shows that the annuity in question could be decomposed into two parts:

• Cash flow today
• The remaining four cash flows are then equivalent to those of an ordinary annuity with a duration of four years (T-1) that starts today and makes the first payment in one year.

To  value the annuity in question, we could, therefore, write:

\( \bf{PV_{\text{Annuity due}} = C + C \times PVIFA_{R,T-1}} = C \times (1+ PVIFA_{R,T-1})\)

For an annuity due that starts today, the relevant PVIFA-factor therefore corresponds to the PVIFA factor of an ordinary annuity (start in one year) with a duration of (T-1) years, plus 1. In our case, the relevant PVIFA factor for an ordinary annuity with a duration of 4 years and a cost of capital of 6% is 3.4651. Consequently, the adjusted PVIFA for an annuity due with duration 5 years is 4.4651:

\( PVIFA(Due)_{R,T} = 1 + PVIFA_{R,T-1} = 1 + 3.4651 = 4.4651 \)

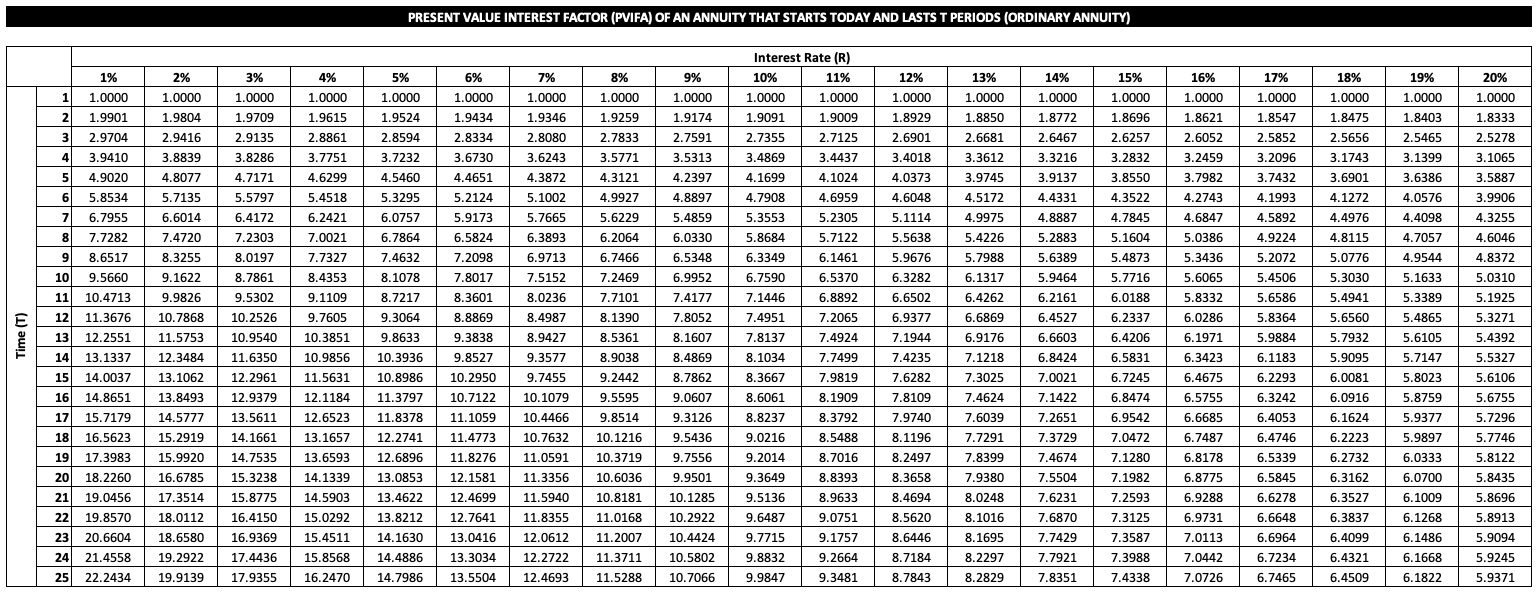
Again, we can represent these PVIFA (Due) factors in a tabular form (click to expand or view the sheet "PVIFA Annuity Due" in the accompanying Excel file):

We can now use this adjusted PVIFA (due) to compute the present value of the total required investment. From today's perspective, the five annual outlays of 250 at the beginning of each year have a value of 1'116.3. 

 \( PV_{\text{Annuity due}} = C \times PVIFA (Due)_{6\%,5} = 250 \times 4.4651 = 1'116.3 \)

Annuity Due: Adjusting the Present Value of an Ordinary Annuity

Alternatively, we can compute the present value of an annuity due as follows:

1. First, use the valuation technique for an ordinary annuity
    
2. Second, adjust the resulting present value to account for the fact that the first cash flow does not occur in one year but already today (or, generally speaking, n years from now).

The following graph illustrates this procedure. We have used the very same "trick" already in the context of perpetuities.

In our example above, the first cash flow occurs today. n therefore takes a value of 0 (today = 0 years from now). The above valuation approach therefore yields:

1. PV ordinary annuity: PV_-1 = C × PVIFA_6%,5 = 250 × 4.2124 = 1'053.10
    
2. PV today: PV₀ = PV_-1 × (1+R) = 1'053.1 × 1.06 = 1'116.3.

This is the same result as in with the first approach, where we have split the annuity due into a cash payment today plus an ordinary annuity.

Generally speaking, the present value of an annuity that starts with a first payment n years (periods) from today, runs for T periods, and is subject to a cost of capital of R is:
 

\( \bf{PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)}} \)

Example 4

An annuity makes an annual payment of 50'000. In total, there are 20 payments and the first payment occurs in 0.4 years. The cost of capital is 5%. Based on this information, what is the present value of this annuity?

We have the following information:

• C = 50'000
• T = 20
• R = 5%
• n = 0.4 (the first payment is 0.4 years from now).

Going back to the original table with the PVIFA for ORDINARY annuities, we find PVIFA_5%,20 = 12.4622. Therefore, the present value of the annuity in question is 641'621:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} = 50'000 \times 12.4622 \times 1.05^{0.6} = 641'621 \)

Example 5

You plan to retire in 20 years. From then on, you want to receive EUR 60'000 per year for 25 years. So the first payment will take place in exactly 20 years and all subsequent payments will come in annual intervals. The interest rate is constant at 2%.

Based on this information, how much money do you need in your retirement account today to finance these future retirement payments, assuming that you make no additional investments or withdrawals between now and your expected retirement in 20 years?

We have the following information:

• C = 60'000
• T = 25
• R = 2%
• n = 20 (first payment 20 years from now)

Using the information from the original table with the PVIFA for ORDINARY annuities, we find PVIFA_2%,25 = 19.5235. Therefore, the necessary account balance today is roughly EUR 804'000:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} \)

\( PV_0 = 60'000 \times 19.5235 \times 1.02^{-19} = 804'090 \)

Example 6

Suppose your current account balance is EUR 1 million. What annual retirement payment could you expect in the example above, if all other information remains the same?

In this modified example, we are looking for the annual cash flow C such that its present value is EUR 1 million:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} = 1 \ million \)

We can find the answer by solving the above expression for C and then plugging in the relevant values:

\( C = \frac{PV_0}{PVIFA_{R,T} \times (1+R)^{(1-n)}} = \frac{1'000'000}{19.5235 \times 1.02^{-19}} = 74'618.5 \)

With a balance of EUR 1 million today, the expected annual pension would therefore be approximately EUR 75'000. Note that, to derive the above result, we have not rounded the PVIFA-value to the fourth decimal point. If we work with the rounded value instead, the result of the above computation would be 74'618.34. The difference is due to rounding errors.

With this knowledge, we are now able to compute the present value of virtually any level annuity. Later on, we will then also briefly discuss how to value annuities with a constant growth rate, so-called growing annuities. However, before turning to these growing annuities, let us look at how to compute the Future Value of (level) annuities.