Lektüre: Annuitäten (Renten)

Beispiel 3

Betrachten wir ein Projekt, das eine jährliche Investition von 250 erfordert. Dieser Investitionsbedarf hat eine Laufzeit von 5 Jahren und ist zu Beginn eines jeden Jahres fällig, beginnend heute. Der Diskontsatz beträgt 6%. Wie hoch ist der Present Value der erforderlichen Gesamtinvestition basierend auf diesen Informationen?

In diesem Beispiel handelt es sich um eine Annuität mit Auszahlungen zu Beginn jeder Investitionsperiode, eine so genannte vorschüssige Annuität. Mit dem Wissen, das wir bisher gewonnen haben, gibt es verschiedene Möglichkeiten, solche Annuitäten zu bewerten.

Vorschüssige Annuität: Cashflow heute plus nachschüssige Annuität mit Laufzeit T-1

In der folgenden Abbildung sind die fünf Zahlungsströme des Projekts dargestellt, die zu Beginn jeder Investitionsperiode auftreten. Sie zeigt, dass die betreffende Annuität in zwei Teile zerlegt werden kann:

• Cashflow heute
• Die verbleibenden vier Zahlungsströme entsprechen dann denen einer gewöhnlichen Annuität mit einer Laufzeit von vier Jahren (T-1), die heute beginnt und in einem Jahr die erste Zahlung leistet.

Um die betreffende Rente zu bewerten, könnten wir also schreiben:

\( \bf{PV_{\text{Vorschüssige Annuität}} = C + C \times PVIFA_{R,T-1}} = C \times (1+ PVIFA_{R,T-1})\)

Für eine heute beginnende Rente entspricht der relevante PVIFA-Faktor daher dem PVIFA-Faktor einer gewöhnlichen Rente (Beginn in einem Jahr) mit einer Laufzeit von (T-1) Jahren, plus 1. In unserem Fall beträgt der relevante PVIFA-Faktor für eine gewöhnliche Rente mit einer Laufzeit von 4 Jahren und einem Kapitalkostensatz von 6 % 3.4651. Folglich ist der angepasste PVIFA für eine fällige Rente mit einer Laufzeit von 5 Jahren 4.4651:

\( PVIFA(Vorschüssig)_{R,T} = 1 + PVIFA_{R,T-1} = 1 + 3.4651 = 4.4651 \)

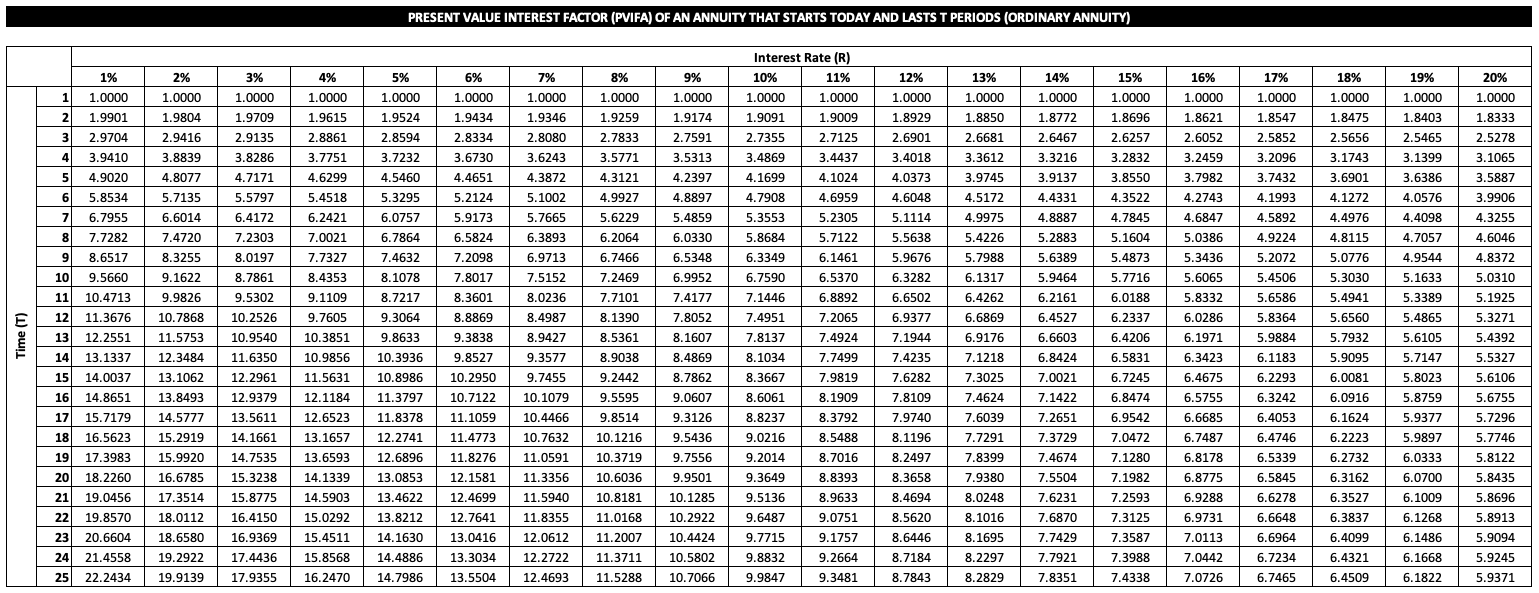
Diese PVIFA-Faktoren für vorschüssige Renten können wir erneut tabellarisch darstellen (vgl. auch das Tabellenblatt "Vorschüssig" in der  Excel-Datei):

Wir können nun diesen angepassten PVIFA-Faktor für vorschüssige Renten verwenden, um den Present Value der gesamten erforderlichen Investition zu berechnen. Aus heutiger Sicht haben die fünf jährlichen Ausgaben von 250 zu Beginn jeden Jahres einen Wert von 1'116.3.    

 \( PV_{\text{Vorschüssige Annuität}} = C \times PVIFA (Vorschüssig)_{6\%,5} = 250 \times 4.4651 = 1'116.3 \)

Vorschüssige Annuität: Den Present Value einer nachschüssigen Annuität anpassen

Alternativ kann der Barwert einer vorschüssigen Annuität wie folgt berechnet werden:

1. Erstens: Anwendung der Bewertungstechnik für eine gewöhnliche (nachschüssige) Annuität

2. Zweitens wird der sich ergebende Barwert angepasst, um der Tatsache Rechnung zu tragen, dass der erste Cashflow nicht in einem Jahr, sondern bereits heute (oder, allgemein gesprochen, in n Jahren) erfolgt

 
Die folgende Grafik veranschaulicht dieses Verfahren. Denselben "Trick" haben wir bereits im Zusammenhang mit ewigen Renten angewandt.

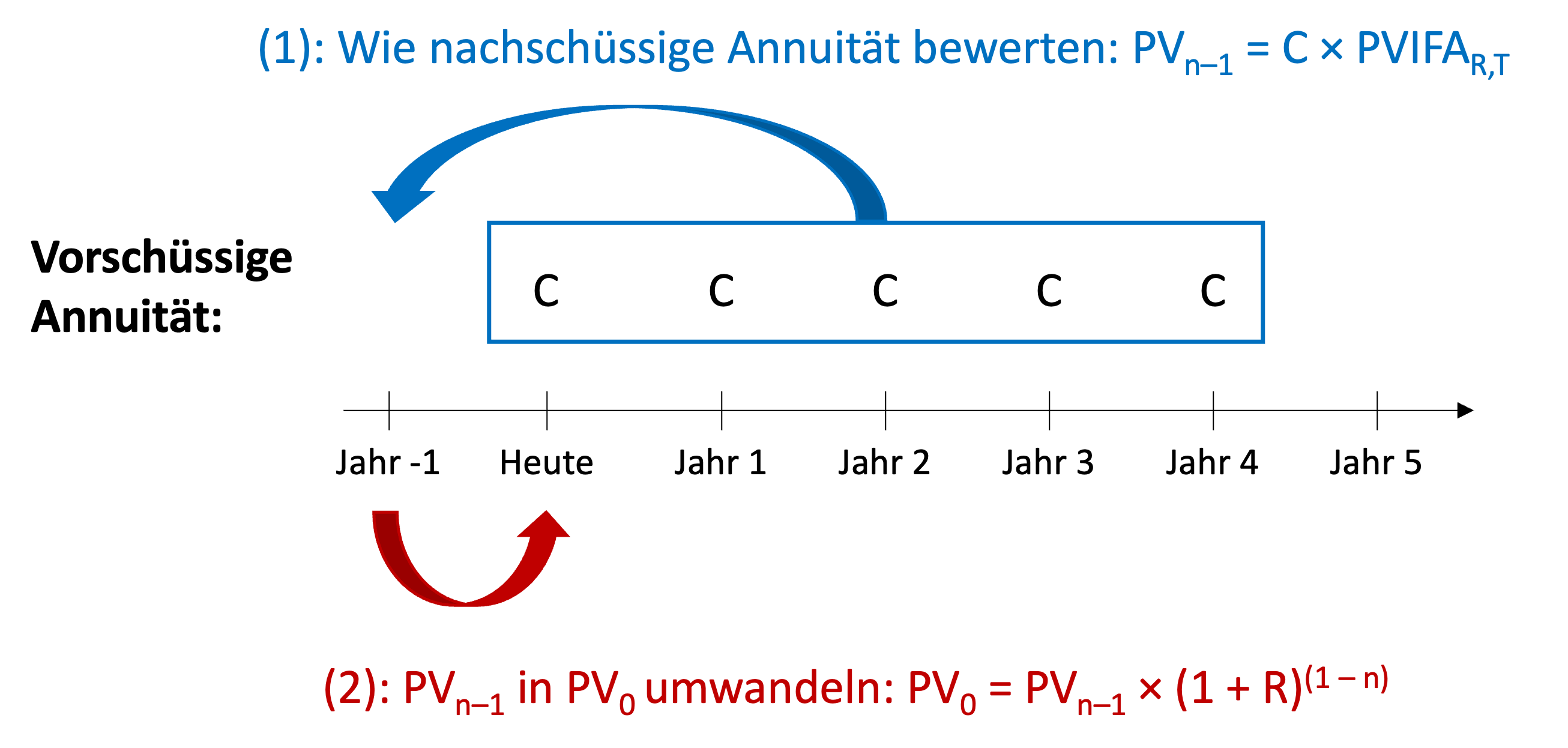
Im Beispiel oben findet der erste Cashflow heute statt. n nimmt deshalb einen Wert von 0 an (heute = 0 Jahre von heute aus). Der oben beschriebene Bewertungansatz liefert das folgende Resultat:

1. PV Vorschüssige Annuität: PV_-1 = C × PVIFA_6%,5 = 250 × 4.2124 = 1'053.10
    
2. PV heute: PV₀ = PV_-1 × (1+R) = 1'053.1 × 1.06 = 1'116.3.

Dies ist dasselbe Ergebnis wie beim ersten Ansatz, bei dem wir die fällige Rente in eine heutige Barzahlung und eine ordentliche Rente aufgeteilt haben.

Im Allgemeinen beträgt der Barwert einer Annuität, die mit einer ersten Zahlung in n Jahren (Perioden) ab heute beginnt, über T Perioden läuft und einem Kapitalkostensatz von R unterliegt:

\( \bf{PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)}} \)

Beispiel 4

Eine Annuität leistet eine jährliche Zahlung von 50'000. Insgesamt gibt es 20 Zahlungen und die erste Zahlung erfolgt in 0.4 Jahren. Der Kapitalkostensatz beträgt 5%. Wie hoch ist der Barwert dieser Annuität?

Wir haben die folgenden Informationen:

• C = 50'000
• T = 20
• R = 5%
• n = 0.4 (die erste Zahlung erfolgt in 0.4 Jahren).

Gehen wir zurück zur ursprünglichen Tabelle mit den PFIVA-Faktoren für nachschüssige Renten, finden wir PVIFA_5%,20 = 12.4622. Der Present Value der fraglichen Rente beträgt also 641'621:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} = 50'000 \times 12.4622 \times 1.05^{0.6} = 641'621 \)

Beispiel 5

Sie planen, in 20 Jahren in Rente zu gehen. Von da an möchten Sie 25 Jahre lang jährlich 60 000 EUR erhalten. Die erste Auszahlung erfolgt also in genau 20 Jahren und alle weiteren Zahlungen erfolgen in jährlichen Abständen. Der Zinssatz liegt konstant bei 2%.

Wie viel Geld müssen Sie heute auf Ihrem Rentenkonto haben, um diese künftigen Rentenzahlungen zu finanzieren, vorausgesetzt, Sie tätigen bis zu Ihrem voraussichtlichen Renteneintritt in 20 Jahren keine zusätzlichen Investitionen oder Entnahmen?

Uns liegen die folgenden Informationen vor:

• C = 60'000
• T = 25
• R = 2%
• n = 20 (die erste Zahlung ist von heute aus in 20 Jahren)

Unter Verwendung der PFIVA-Faktoren für nachschüssige Renten finden wir PVIFA_2%,25 = 19.5235. folglich ist der nötige Kontostand rund EUR 804'000:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} \)

\( PV_0 = 60'000 \times 19.5235 \times 1.02^{-19} = 804'090 \)

Beispiel 6

Angenommen, Ihr Guthaben auf dem Konto beträgt 1 Million EUR. Welche jährliche Rentenzahlung könnten Sie im obigen Beispiel erwarten, wenn alle anderen Informationen gleich bleiben?

In diesem abgewandelten Beispiel suchen wir den jährlichen Cashflow C so, dass sein Barwert 1 Mio. EUR beträgt:

\( PV_0 = C \times PVIFA_{R,T} \times (1+R)^{(1-n)} = 1 \ Mio. \)

Wir können die Antwort finden, indem wir den obigen Ausdruck nach C auflösen und dann die entsprechenden Werte einfügen:

\( C = \frac{PV_0}{PVIFA_{R,T} \times (1+R)^{(1-n)}} = \frac{1'000'000}{19.5235 \times 1.02^{-19}} = 74'618.5 \)

Bei einem heutigen Guthaben von 1 Mio. EUR würde die erwartete jährliche Rente also etwa 75 000 EUR betragen. Beachten Sie, dass wir zur Ableitung des obigen Ergebnisses den PVIFA-Wert nicht auf die vierte Dezimalstelle gerundet haben. Wenn wir stattdessen mit dem gerundeten Wert arbeiten, würde das Ergebnis der obigen Berechnung 74'618.34 betragen. Die Differenz ist auf Rundungsdifferenzen zurückzuführen.

Mit diesem Wissen sind wir nun in der Lage, den Present Value praktisch jeder konstanten Annuität zu berechnen. Später werden wir auch kurz erörtern, wie man Annuitäten mit einer konstanten Wachstumsrate, die so genannten wachsenden Annuitäten, bewertet. Bevor wir uns jedoch diesen wachsenden Annuitäten zuwenden, wollen wir uns ansehen, wie man den Future Value von (konstanten) Annuitäten berechnet.