Reading: Annuities
3. Future Value of Annuity
Oftentimes, we also want to know how much money we can expect to have at the end of an investment project that takes the form of an annuity. For example, in the case of retirement planning, an investor could be interested to know the expected available balance upon retirement if she makes annual contributions of, say, $10'000 at a constant rate of return. The Future Value of an Annuity provides the answer to such questions.
With all the compounding and discounting knowledge that we have accumulated so far, it should not be a big challenge to derive this future value. To start, let us consider ordinary annuities which make the first payment in exactly one year (investment period).
The Future Value of Ordinary Annuities
In keeping with our notation form before, T denotes the end of an ordinary annuity. If we are interested in the future value of an annuity at its ending, we are therefore looking for a future value that is T investment periods from now. We can find that future value by compounding the Present Value of an Annuity over T periods:
\( FV_T = PV_0 \times (1+R)^T \)
Remember that PV0 of the annuity is: \( PV_0 = C \times PVIFA_{R,T} \) and that PVIFAR,T is \( PVIFA_{R,T}=\frac{1-(1+R)^{-T}}{R} \). Consequently, we can write:
\( FV_T = C \times PVIFA_{R,T} \times (1+R)^T = C \times \frac{1-(1+R)^{-T}}{R} \) \( \times (1+R)^T \)
This simplifies to the following expression for the future value of ordinary annuities with duration T and a discount rate R:
\( \bf{FV_T = C \times \frac{(1+R)^T-1}{R}} \)
The latter term, \( \frac{(1+R)^T-1}{R} \) is generally referred to as the Future Value Interest Factor of an Annuity, short FVIFA. Consequently:
\( \bf{FV_T = C \times FVIFA_{R,T}} \)
with: \( \bf{FVIVA_{R,T} = \frac{(1+R)^T-1}{R}} \)
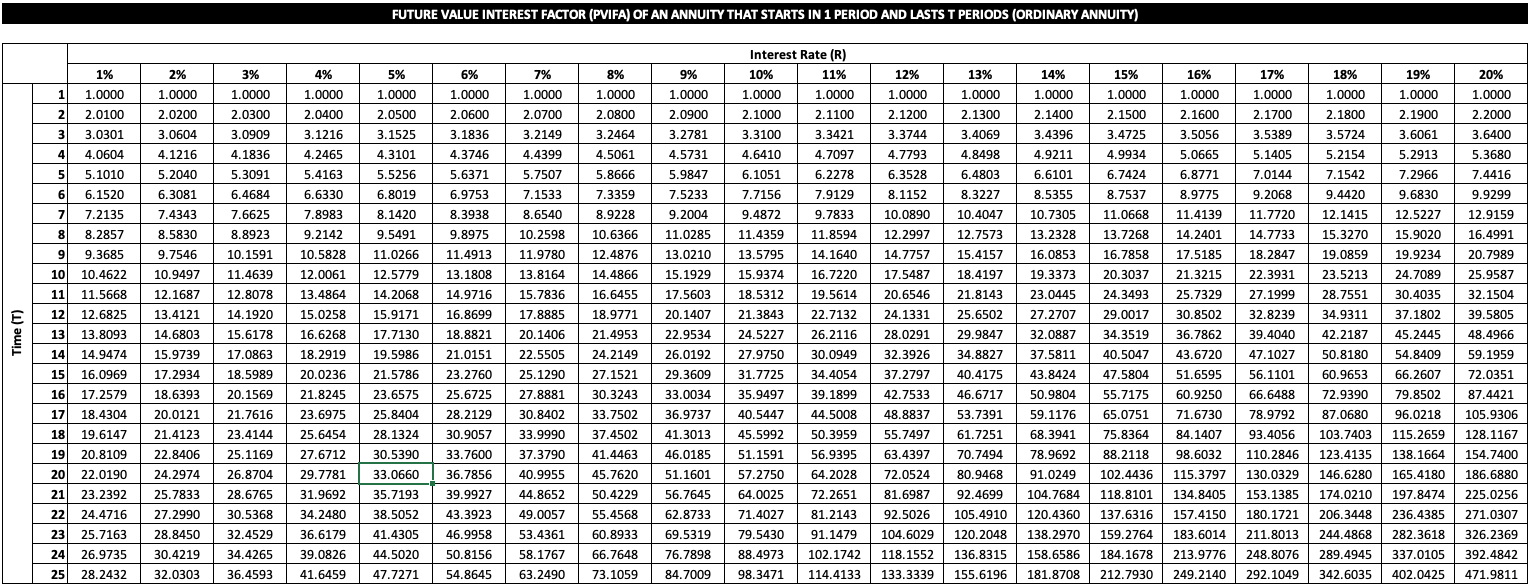
As in the case of the PVIFA, the FIVA solely depends on the duration of the annuity (T) and the interest rate (R). Therefore, we can also express FVIFA in a simple two-way table (click to enlarge or see the accompanying Excel file):
Example 6
An investor is planning to put aside GBP 15'000 each year for the next 10 years. The first savings payment will be in exactly 1 year and all subsequent payments will be made in annual intervals. The interest rate is 4%. Based on this information, what's the expected account balance at the end of the savings period, 10 years from now?
We have the following information:
- C = EUR 15'000
- T = 10
- R = 4%.
Based on this information, we can determine the appropriate FVIFA using the table above, namely 12.0061. Consequently, the future value of this annuity is GBP 180'092:
\( FV_{10} = C \times FVIFA_{4\%,10} = 15'000 \times 12.0061 = 180'092 \)
This is the basic approach to compute the future value of an ordinary annuity. Regardless of starting point, this approach computes the future value at the time of the last payment of the annuity (no interest on the last annuity payment).
Future Value of Annuity Due
The approach discussed above computes the future value of the annuity at the time of the last payment, regardless of the starting point:
- In Example 6, the last payment is 10 years from now, so the future value is also 10 years from now.
- In contrast, if the annuity in question was an annuity due with payments at the beginning of each investment period, the last payment would occur 9 years from now, at the BEGINNING of year 10, so that the future value would also be 9 years from now.
If we are interested in the future value of an annuity due at the end of the last investment period, we can adjust the calculations from above accordingly. In keeping with the notation from preceding sections, we use the variable n to denote the time between the start of the annuity and the first payment. In the context of future values of annuities, n can take any value between 0 and 1:
- n = 0: First payment at the start of the investment period. This is an Annuity Due.
- n = 1: First payment at the end of the investment period. This is an Ordinary Annuity.
To get the future value at the end of the last investment period, the generalized computation is:
\( \bf{FV_{T} = C \times FVIFA_{R,T} \times (1+R)^{(1-n)}} \)
Example 7
Today is your 30st birthday. You decide to open an account to start saving for a massive party for your 50st birthday. You deposit CHF 5'000 today and you plan to invest another CHF 5'000 on each of your following birthdays until you turn 49. On your 50st birthday, you then liquidate the account and throw a party. The interest rate is 3%. What's the budget for your party?
In this example, we have:
- n = 0 (the first payment is today, at the beginning of the investment period)
- C = 5'000
- T = 20 (you make a total of 20 deposits)
- R = 3%.
As we have mentioned above, the standard approach to value annuities with the FVIFA table shown above (FVIFA3%,20 = 26.8704) will compute the future value at the time of the last investment payment, i.e., right after your deposit on the 49th birthday, the beginning of your 20th investment period. Since you are interested in the balance one year later (i.e., on your 50th birthday, the end of the 20th investment period), you adjust the resulting FV by compounding it over 1 year:
\( FV_{T} = C \times FVIFA_{R,T} \times (1+R)^{(1-n)} = 5'000 \times 26.8704 \times 1.03^{1-0} = 138'382 \)
Based on this information, you can expect to have a budget of roughly CHF 138'000 for your birthday party.