Reading: Net Present Value (NPV)

Example 1

Suppose you can buy a piece of land outside of New York for $900'000 today. Based on your market research, you assume that you will be able to sell that land in one year for $1.1 million. Alternatively, you could invest your money in a project with identical risk at a rate of return of 10%. Should you buy the land?

In the example, we know the expected future value of the land in 1 year, namely $1.1 million (C₁). We also know today's price, namely $0.9 million, as well as the risk-adjusted rate of return (R) that we could achieve elsewhere (10%). What we do not know yet, however, is the fair value of the land from today's perspective: What's the present value of a project that pays $1.1 million in a year and commands a return of 10%?  Is it smaller or larger than the asking price of $0.9 million? To find out, we can compute the present value (PV) of the expected sales price in 1 year (C₁):

\( PV = \frac{C_1}{1+R}=\frac{1'100'000}{1.1} = 1'000'000 \).

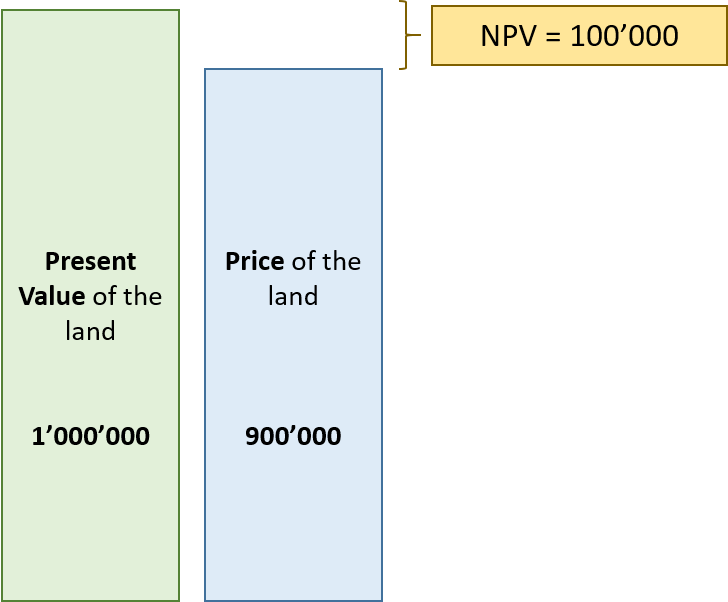
The present value of the land is $1 million. However, this does not imply that you are $1 million better off by buying the land, since you first have to invest $0.9 million today in order to purchase the land. Net of this investment, the value of the land therefore is 100'000. This is the so-called Net Present Value (NPV):

NPV = −Investment today + PV = − 900'000 + 1'000'000 = 100'000.

The interpretation is straightforward: The land is $100'000 worth more than it costs. By buying it, the project makes a net contribution of $100'000 to your wealth:

More formally, the expression to compute the NPV of the project can be written as:

\( NPV = C_0 + \frac{C_1}{1+R} = -900'000 + \frac{1'100'000}{1.1} = 100'000 \),

 where C₀ is the investment we make today and therefore assumes a negative value (cash outflow).

In this particular case, it is therefore worthwhile to undertake the project, since you buy an asset at $900'000 that is worth $1'000'000.

Example 2

Let's consider another investment proposal. Suppose you can invest 500 today in a project that generates a cash flow of 300 in 1 year and 400 in 2 years. The opportunity cost of capital is 10%. Should you go ahead with the project?

To find the answer, we have to compare the present value of the investment (C₀ = -500) with the present value of the future cash flows (300 in 1 year and 400 in 2 years):

\( NPV = C_0 + PV = C_0 + \left( \frac{C_1}{(1+R)} + \frac{C_2}{(1+R)^2} \right) = -500 + \left( \frac{300}{1.1} + \frac{400}{1.1^2} \right) \)

\( NPV = -500 + (272.7 + 330.6) = -500 + 603.3 = 103.3 \)

In words: On aggregate, the cash flows of year 1 and year 2 have a present value of 603.3. This present value of the future cash flow exceeds today's investment of 500 by 103.3. Consequently, the net present value (NPV) of the project is 103.3. By conducting the project, your net worth should increase by 103.3 (you buy for 500 an asset that has a value of 603.3 today).