Lektüre: Net Present Value (NPV)

Beispiel 1

Nehmen wir an, Sie können heute ein Stück Land ausserhalb von New York für $900'000 kaufen. Basierend auf Ihrer Marktforschung gehen Sie davon aus, dass Sie dieses Grundstück in einem Jahr für $1.1 Mio. verkaufen können. Alternativ könnten Sie Ihr Geld auch in ein Projekt mit identischem Risiko und einer Rendite von 10% investieren. Sollten Sie das Grundstück kaufen?

In diesem Beispiel kennen wir den erwarteten zukünftigen Wert des Grundstücks in einem Jahr, nämlich $1.1 Mio. (C₁). Wir kennen auch den heutigen Preis, nämlich $0.9 Mio., sowie die risikobereinigte Rendite (R), die wir anderswo erzielen könnten (10%). Was wir jedoch noch nicht kennen, ist der heutige "faire" Marktwert des Grundstücks: Wie hoch ist der Present Value eines Projekts (in unserem Fall ein Grundstück), das in einem Jahr $1.1 Mio. einbringt und Kapitalkosten von 10% aufweist?  Wir können den fairen Wert bestimmen, indem wir den Present Value (PV) des erwarteten Verkaufspreises in einem Jahr (C₁) berechnen:

\( PV = \frac{C_1}{1+R}=\frac{1'100'000}{1.1} = 1'000'000 \).

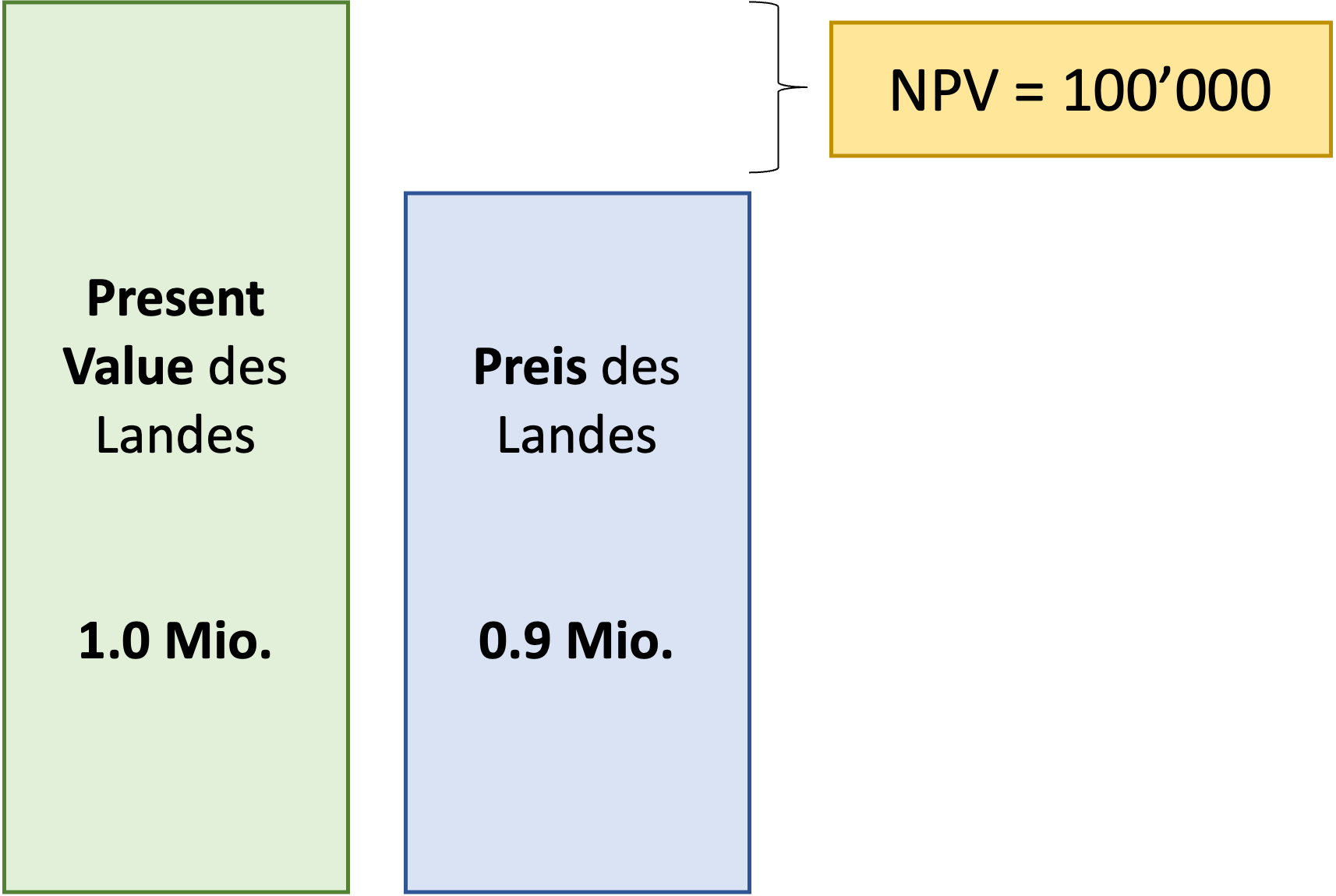
Der Present Value des Grundstücks beträgt $1 Mio. Folglich können Sie heute für $0.9 Mio. ein Grundstück erwerben, das einen fairen Marktwert von $1.0 Mio. aufweist. Wenn Sie dieses Geschäft tätigen, erhöht sich Ihr Nettovermögen um $0.1 Mio. Dies ist der Net Present Value (NPV) des Projekts. Er berechnet sich als der Present Value aller zukünftigen Cashflows abzüglich der heute nötigen Investition:

NPV = −Investition heute + PV zukünftige Cashflows = − 900'000 + 1'000'000 = 100'000.

Die Interpretation des NPV ist einfach: Das Grundstück ist $100'000 mehr wert als es kostet. Durch den Kauf leistet das Projekt einen Nettobeitrag von $100'000 zu Ihrem Vermögen:

Formal kann der Ausdruck zur Berechnung des Net Present Values des Projekts wie folgt geschrieben werden:

\( NPV = C_0 + \frac{C_1}{1+R} = -900'000 + \frac{1'100'000}{1.1} = 100'000 \),

 wobei C₀ die Investition ist, die wir heute tätigen, und daher einen negativen Wert annimmt (Mittelabfluss).

Im betrachteten Fall lohnt es sich also, das Projekt durchzuführen, da Sie für 900'000 $ einen Vermögenswert kaufen, der 1'000'000 $ wert ist.   

Beispiel 2

Betrachten wir einen anderen Investitionsvorschlag. Angenommen, Sie können heute 500 in ein Projekt investieren, das in einem Jahr einen Cashflow von 300 und in zwei Jahren einen Cashflow von 400 einbringt. Die Opportunitätskosten des Kapitals betragen 10%. Sollten Sie das Projekt in Angriff nehmen?

Um die Antwort zu finden, müssen wir den Gegenwartswert der Investition (C₀ = -500) mit dem Gegenwartswert der künftigen Cashflows (300 in einem Jahr und 400 in zwei Jahren) vergleichen:

\( NPV = C_0 + PV = C_0 + \left( \frac{C_1}{(1+R)} + \frac{C_2}{(1+R)^2} \right) = -500 + \left( \frac{300}{1.1} + \frac{400}{1.1^2} \right) \)

\( NPV = -500 + (272.7 + 330.6) = -500 + 603.3 = 103.3 \)

In Worten: Die Zahlungsströme des Jahres 1 und des Jahres 2 haben zusammen einen Gegenwartswert von 603.3. Dieser Gegenwartswert des künftigen Cashflows übersteigt die heutige Investition von 500 um 103.3. Folglich beträgt der Net Present Value (NPV) des Projekts 103.3. Mit dem Projekt dürfte sich Ihr Reinvermögen um 103.3 erhöhen (Sie kaufen für 500 einen Vermögenswert, der heute einen Wert von 603.3 hat).