Reading: Unlevering and Relevering Betas
1. Setting the Stage
The previous considerations have shown that a levered firm has two sources of value:
- The operating business (VU)
- The financing policy (due to debt tax shields, DTS)
Earlier in the module (in the section Financial Leverage and the Cost of Capital) we have already discussed the basic relations between the overall cost of capital, financial leverage, and the cost of equity. With this, we are, in principle, ready to estimate the cost of capital (especially kE and WACC) under any financing policy.
The approach we chose to match the firm's cost of capital to it's financing policy was to first "unlever" the cost of capital (estimate kA) and then relever it to the new financing policy (estimate kE*, WACC). While this is arguably the simplest and most intuitive way to do it, most textbooks and practitioners choose a slightly different approach: They "unlever" and "relever" the RISK of the different sources of capital, i.e., the beta coefficients from the Capital Asset Pricing Model (CAPM).
Because "unlevering" and "relevering" is such an important part of the cost of capital estimation, the purpose of this appendix is to:
- Consolidate the various approaches to unlevering and relevering the cost of capital
- Show that all these approaches yield the same result (that is, it does not matter whether you unlever and relever the cost of capital or the betas)
- Show that the simplified approaches most textbooks and practitioners use lead to substantial bias in the cost of capital estimation.
The starting point for our considerations is a simple balance sheet at market values:
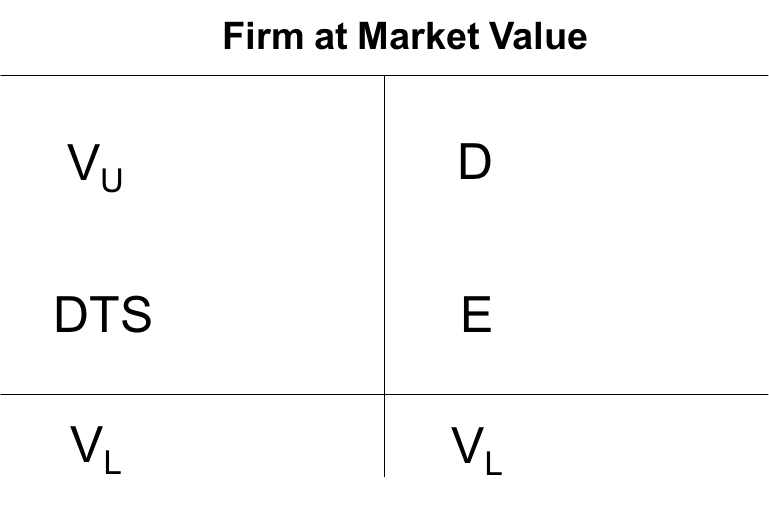
This balance sheet simply states that the overall value of the firm (Levered firm value, VL) reflects the market value of the firm's operating business (VU) and its financing policy (DTS). This value must correspond to the total value of the financial claims against the firm, in our case net debt (D, debt outstanding minus excess cash) and equity (E).
VL = VU + DTS = D + E.
Now let us look at the various approaches of unlevering and relevering. In doing so, we must think about the riskiness of the various ingredients of the above equation as well as their implied cost of capital.
We have already talked in detail about the riskiness of debt and equity. In particular, we have derived the cost of debt (kD) and the cost of equity (kE) and we have discussed how to use the Capital Asset Pricing Model (CAPM) to estimate the cost of capital of any financial asset j as a function of its riskiness (beta, β):
kj = RF + βj × Market risk premium.
What we have not yet taken about explicitly is the riskiness of the firm's debt tax shield (DTS) and, consequently, the appropriate discount rate to capitalise the future tax savings the firm can generate with its interest payments.
With respect to the riskiness of the debt tax shield, there are two popular assumptions:
- The debt tax shield has the same risk as the firm's debt. Consequently, the beta of the DTS is βD and the appropriate cost of capital to discount future interest savings is kD.
- The debt tax shield has the same risk as the firm's assets. Consequently, the beta of the DTS is βA and the appropriate cost of capital to discount future interest savings is kA.
While the two assumptions are approximately equally popular in the available textbooks, it is important to note that we should not randomly choose between the two. There are situations in which the first approach (risk of DTS is equivalent to risk of debt) is more suitable; and there are situations in which the latter approach (risk of DTS is equivalent to risk of assets) is more suitable.
Very generally speaking, firms can pursue two types of financing policies (or a mixture thereof):
- They can pursue a target debt ratio: This means that they borrow a more or less constant percentage of firm value (say, for example, debt is 40% of firm value). What are the implications of such a financing policy?
-
- Firms borrow more if the value of the firm goes up; and they borrow less if the value goes down.
- Debt outstanding, therefore, fluctuates with the value of the operating business.
- Therefore, also the tax savings fluctuate with the value of the operating business.
- If debt tax savings fluctuate with the value of the operating business, we should capitalize them with a cost of capital that reflects the riskiness of the operating business!
Policy implications: If firms pursue a target debt ratio, it is reasonable to assume that the DTS has the same risk as the firm's assets. Consequently, the beta of the DTS is βA and the appropriate cost of capital to discount future interest savings is kA.
- Alternatively, firms could strive for some target debt levels (in currency): This means that they borrow a specific amount of debt (say, 10 million) and do not «constantly» adjust debt outstanding in reaction to changes in the business model. What are the implications of such a financing policy?
- Debt outstanding is less directly related to the fluctuations of business operations
- Whether or not the firm can pay interest (and cash the associated tax savings) is more or less driven by its credit risk.
- This credit risk is approximately summarized by βD and the corresponding cost of capital is kD.
Policy implications: If firms pursue a target debt levels (in currency), it is reasonable to assume that the DTS has the same risk as the firm's debt. Consequently, the beta of the DTS is βD and the appropriate cost of capital to discount future interest savings is kD.
In what follows, we look at how to unlever and relever the betas and the cost of capital under these two assumptions.