Reading: Introduction to Firm Valuation

Ultimately, we want to develop a framework that allows us to estimate the fair market value of any asset and to understand how specific decisions we take affect that value. In this course, the "asset” we consider is the firm as well as the financial claims on it. Put differently, we want to be able to estimate the value of a firm, the value of its debt and equity, as well as its fair share price. We also want to understand how corporate actions such as mergers and acquisitions, share repurchases, or changes in the financing policy affect value.

The basic principle behind our considerations is fairly simple: The market value of any financial asset corresponds to the present value of all future net cash flows the owner of that asset expects to collect.

The analysis therefore focuses on two main questions:

1. How much cash will the asset (or the management decision) generate in the future?
     
   
2. What's the value of cash collected in the future?

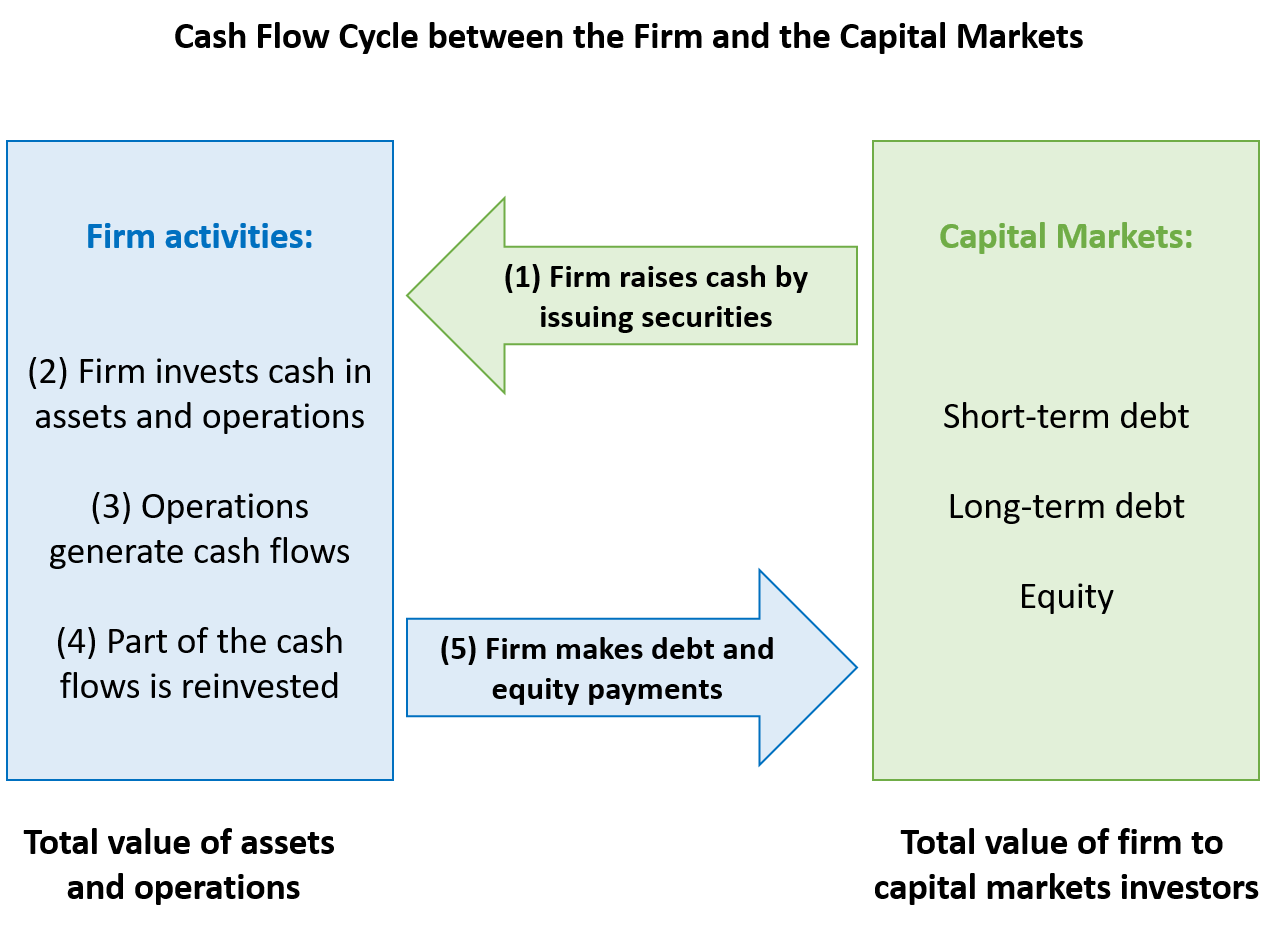
At the firm level, the financial plan should contain the relevant information about the firm's future ability to generate cash. To answer the first question above, we therefore have to be able to compile and understand financial plans. This means that we have to know the basic principles of accounting as well as the financial statements. And we need to understand the cash flow cycle between capital markets and the firm in question. Put differently, we need to be able to determine:

1. How much cash the firm raises from capital markets by issuing securities.
    
   
2. How the firm invests this cash in real assets.
    
   
3. How much cash the firm generates from operating these assets.
    
4. How much of the generated cash is reinvested in the business.
    
5. And how much cash will be returned to the providers of capital via debt and equity payments.

The following graph summarizes this simplified cash flow cycle between the firm and the capital markets:

Using the logic outlined above, financial market participants will therefore compare the cash they invest in the firm (step 1 in the graph above) with the cash they receive from the firm (step 5 in the graph above) to find an answer to the first main question raised above.
     

To answer the second main question above, we need to know the so-called time value of money. Put differently, we need to understand which return the providers of capital require in exchange for investing capital in the firm. The answer to that question will depend on the timing of the cash flows as well as their riskiness.

All of these issues will be discussed in great details throughout this course. Before taking a closer look at how we proceed, let us present a simple example that illustrates how to bring cash flows and time value of money together in order to estimate the financial value of a firm.

1. How much cash will the firm generate in the future? We expect the firm to generate 1'100 in exactly 1 year and 1'210 in exactly 2 years. Thereafter, the firm will not generate any additional cash flows.
    
2. What's the value of cash collected in the future? We assume that the providers of capital require an annual rate of return of 10%.

Based on this information: What is the value of this firm?

Let's look at the firm's two cash flows separately. The first cash flow (CF) of 1'100 arrives in 1 year. We know that, instead of investing in the company, the providers of capital could invest their money at an annual rate of return of 10%. Let's denote this return with the letter k. Hence, to get a cash flow of 1'100 in 1 year with this alternative investment, the investors would have to invest 1'000 today: 1'000 × (1+0.1) = 1'100. This is the so-called present value. The promise to get 1'100 in 1 year has a value of 1'000 today. This is because the investor can replicate the payment of 1'100 in 1 year by investing 1'000 today in the alternative investment opportunity. Formally:

Present Value (PV)₁= \( \frac{CF_1}{(1+k)^1}=\frac{1'100}{1.1} \) =1'000.

The situation is very similar with respect to the second cash flow. The only notable difference is that that cash flow arrives in two years instead of one. To replicate a payment of 1'210 in two years with the alternative investment, the provider of capital has to invest another 1'000 today: 1'000 × (1+0.1)^2 = 1'210. Therefore, the present value of the second payment is 1'000 as well:

Present Value(PV)₂ = \(\frac{CF_2}{(1+k)^2}=\frac{1'210}{1.1^2} \) = 1'000.

Once we have computed the value of each cash flow, we find the overall value of the firm by simply adding up the individual present values:

Firm value = \( \frac{CF_1}{(1+k)^1}+\frac{CF_2}{(1+k)^2}=\frac{1'100}{1.1^1}+\frac{1'210}{1.1^2} \) =1'000+1'000=2'000.

Interpretation: The promise to receive 1'100 in 1 year and 1'210 in two years has a value of 2'000. The reason is that the investor could put the 2'000 in the alternative investment and exactly replicate the cash flow profile of the company. In other words: If we buy the company at 2'000 today, we expect to earn an annual return of 10% on this investment.

The general form to obtain the present value of a stream of T future payments is:

Present Value = \( \frac{CF_1}{(1+k)^1}+\frac{CF_2}{(1+k)^2}+\frac{CF_3}{(1+k)^3}+...+\frac{CF_T}{(1+k)^T}=\sum\frac{CF_t}{(1+k)^t} \).

This is the basic principle of corporate finance. To value an asset, we (1) determine the cash flows associated with owning that asset and (2) compute the present values of these cash flows based on the investors' required rate of return. We (3) find the value of the asset by summing up the individual present values. The process of computing present values of future cash flows is called discounting. This is why the valuation approaches that rely on this basic principle are called discounted cash flow (DCF) valuation approaches.

The following figure illustrates the DCF approach:

Clearly, the mechanics of basic valuation are fairly simple. Yet they are remarkably powerful. 

In the following chapter, we apply this simple logic to a real life company. This will allow us to set the stage for firm valuation and outline the logic of this course in more detail.