Growth and Investment in the Steady State
This section discusses the crucial issue of how to assess the firm value created after the explicit forecast period.
1. Growth and Investment in the Steady State
Firms go through various phases during their lives. Often, the start-up phase is characterized by large new investments and slow growth. In a second phase, growth becomes explosive. Eventually, however, many firms (not all!) converge to a steady state where they achieve a moderate growth rate that is supported by replacement investments and, potentially, new investments. We want to examine the implications of such a steady state for firm valuation.
In the long run, the following considerations seem economically reasonable:
- Over time, competition washes away the real growth opportunities of the firm's assets in place.
- Therefore, the growth rate g the firm can achieve with its assets in place (current operations) eventually converges to the rate of inflation, denoted with the greek letter π.
- Firms can only survive in the long run if they maintain their assets in place. Maintaining the assets in place means that they engage in replacement investments that equal depreciation.
- If firms only maintain their assets in place (replacement investments = depreciation), the current operations remain the same and the growth rate converges to the rate of inflation π.
- If the firm wants to achieve real growth, it has to make new investments (in excess of depreciation) to capture new growth opportunities. We denote the return the firm earns on these new investments with ROIC (return on incremental capital).
These considerations imply that, in the steady state, the firm's growth rate and investment policy are not independent. The current operations are expected to grow at the rate of inflation whereas new investments will generate a growth rate of ROIC:
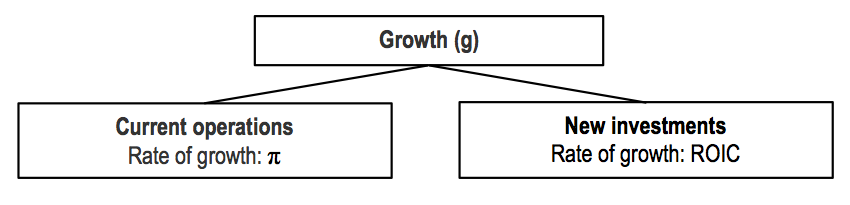
Therefore, the long-term growth rate depends on how much the firm invests into new growth opportunities and the return it earns on these growth opportunities. If we express the new investments as a fraction p of the firms (operating) net income NOPLAT, we can write:
\( g = (1-p) \times \pi + p \times ROIC \).
p is the so-called reinvestment (or plowback) rate of new investments. The above expression simplifies to:
\( g = \pi + p \times (ROIC- \pi) \).
This equation summarizes the main takeaways from before: If the firm only conducts replacement investments and makes no new investments (p = 0), it is reasonable to expect a growth rate that corresponds to the rate of inflation. In the long run, real growth only comes from new investments (p > 0) on which the firm earns a real return of (ROIC - π).
If we assume that managers never invest in projects with negative NPV, then we know that ROIC cannot be smaller than the WACC. To be sustainable, however, the ROIC cannot be much larger than the WACC either, otherwise there will be entry and imitation by competitors. Plausible assumptions could be ROIC = WACC over the long run in very competitive industries, and ROIC = WACC + 1% otherwise.
The key takeaways of these considerations are:
- Growth is a function of the firm's new investment opportunities (ROIC) as well as its investment policy (p).
- In the steady state, the firm makes replacement investments which correspond to the depreciation charges.
- If the firm does not make any new investments (p = 0) it is reasonable to assume that the long-term growth rate equals the rate of inflation: g = π.
- If the firm has no new projects with positive net present value, ROIC is smaller than WACC and new investments destroy value (even though the firm may still grow). Therefore, the firm should not make any new investments and set p = 0.
As we have seen, these considerations have important implications for the rate of growth that we assume in the steady state: Arguably, the lower bound for a sustainable long-term growth rate g is the expected rate of inflation \( \pi \). Equally importantly, logic also dictates an upper bound for g. Remember that the model we use for the steady state is that of a growing perpetuity. In the very long run (= forever), a firm cannot grow faster than the global economy. Otherwise, it would continuously increase its market share of the global economy and, ultimately, have to expand to other planets and galaxies in order to keep growing faster than the world economy. Therefore, the upper bound of the long-term growth rate g is set by the long-term expected global GDP (gross domestic product) growth rate.
In the steady state, we therefore have:
\( \pi \leq g \leq GDP \space growth \)
Whether the growth rate is closer to the rate of inflation or (global) GDP growth depends on the availability of valuable growth opportunities.
Let's have a look at a few examples to get more familiar with these considerations:
Example 1: Suppose a firm is able to find projects with a ROIC of 1% above the WACC of 10%. The firm expects to reinvest 40% and the expected rate of inflation is 3%. What's the firm's expected growth rate?
From before, we know: \( g = \pi + p \times (ROIC- \pi) \).
In our case, the firm has the following characteristics:
- ROIC = WACC + 1% = 11%
- p = 40%
- π = 3%.
Therefore, its expected rate of growth is 6.2%:
\( g = \pi + p \times (ROIC- \pi) = 0.03 + 0.4 \times (0.11 - 0.03) \) = 6.2%.
Example 2: Now the same firm wants to grow at 8% per year (assuming this growth rate is below the expected GDP growth rate). What fraction of NOPLAT would it have to reinvest into now project if all other parameters remain the same?
We can solve our expression of the firm's growth rate for the reinvestment rate p:
\( g = \pi + p \times (ROIC - \pi) \rightarrow p=\frac{g- \pi}{ROIC - \pi} \).
If the target growth rate g is 8%, the required reinvestment rate p is 62.5%:
\( p=\frac{g- \pi}{ROIC - \pi} = \frac{0.08-0.03}{0.11-0.03} = 0.625 \).
Example 3: A firm can invest 50% of NOPLAT in projects that generate a ROIC of 8%. The long-term rate of inflation is 3% and the firm's WACC is 10%. What's the firm's expected growth rate?
The wrong answer would be 5.5%:
\( g = \pi + p \times (ROIC- \pi) = 0.03 + 0.5 \times (0.08 - 0.03) \) = 5.5%.
Why is this answer wrong? The reason is that new investments seem to destroy value in this particular company, as the return they generate (ROIC = 8%) is not sufficient to cover the cost of capital (WACC = 10%). Therefore, the firm should not make any new investments and set p = 0. In that case, the firm will only grow at the rate of inflation of 3%:
\( g = \pi + p \times (ROIC- \pi) = 0.03 + 0 \) = 3.0%.
This example illustrates that growth is not equal to value creation. The firm can accelerate its growth by investing into projects that destroy value (ROIC < WACC). A more sustainable investment policy, however, is to abstain from new investments and return the capital to the shareholders instead. While this alternative investment policy brings about slower growth, it does not destroy value.