Reading: Unlevering and Relevering Betas

The figure below shows the components of the balance sheet at market value as well as the associated risk measures (in blue).

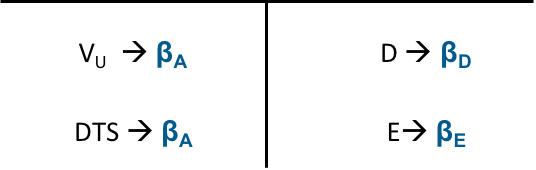
Since this is a balance sheet, we know that the overall risk of the left-hand side (V_U and DTS) must correspond to the overall risk of the right-hand side (D and E). Consequently:

\( \beta_A \times V_U + \beta_A \times DTS = \beta_D \times D + \beta_E \times E \).

Remember from the previous page that:

\( V_L = V_U + DTS = D + E \).

Consequently, we can rewrite the above expression as:

\( \beta_A \times (V_U + DTS) = \beta_D \times D + \beta_E \times E \);

\( \beta_A \times V_L = \beta_D \times D + \beta_E \times E \);

\( \beta_A \times (D + E) = \beta_D \times D + \beta_E \times E \).

We find the risk of the firm's assets (β_A) by dividing the equation with (D+E):

\( \beta_A = \beta_D \times \frac{D}{D+E} + \beta_E \times \frac{E}{D+E} \).

In words: The overall risk of the firm's assets (β_A) is the weighted average of the risks of its debt (β_D) and equity (β_E). Under the assumption that the DTS falls in the risk class of the firm's assets, this is the appropriate expression to unlever the equity beta.

Many textbooks and practitioners make the simplifying assumption that the beta of debt (β_D) is zero. If we set β_D = 0, the above expression simplifies to:

 \( \beta_{A, simplified} = \beta_E \times \frac{E}{D+E} \)

With this simplified assumption, we find the unlevered beta (β_A) by multiplying the levered beta (β_E) with the firm's current equity ratio (E/(D+E)).

If we then want to estimate the equity beta under a different target capital structure (*), we have to relever the cost of capital. We can do so by solving the above expressions for β_E. After some rearrangements, we find for the full version:

\( \beta_E^* = \beta_A + (\beta_A - \beta_D^*) \times \big(\frac{D}{E}\big)^* \) 

and for the simplified version, where we assume that β_D = 0:

\( \beta_{E, simplified}^* = \beta_A \times \big(\frac{D+E}{E}\big)^* \)

The latter expression is, again, rather easy to interpret: to find the equity beta under the new capital structure (*), simply divide the unlevered beta by the target equity ratio.

Example: Consider a firm with the following characteristics:

• Current debt ratio (D/(D+E)) = 20%
• Current equity ratio (E/(D+E)) = 80%
• Current equity beta (β_E) = 1.5
• Current debt beta (β_D) = 0.4
• Target debt ratio (D/(D+E))* = 60%

We want to find the risk of the firm's equity under the new capital structure (β_E*):

The first step is to compute the unlevered beta (β_A) under the current financing policy. Using the equations from above, we find:

\( \beta_A = \beta_D \times \frac{D}{D+E} + \beta_E \times \frac{E}{D+E} = 0.4 \times 0.2 + 1.5 \times 0.8 = 1.28 \).

This beta we can now re-lever to the firm's target capital structure. To do so, we have to understand how the change in financing policy will affect the firm's credit terms. Let us assume, that the substantial increase in the debt ratio from 20% to 60% makes debt riskier. Therefore, the risk factor associated with debt, β_D, increases from 0.4 to 0.6 (more on this later):

\( \beta_E^* = \beta_A + (\beta_A - \beta_D^*) \times \big(\frac{D}{E}\big)^* = 1.28 + (1.28 - 0.6)\times \big(\frac{0.6}{0.4}\big) = 2.3\).

In words: The substantial increase in debt financing (from 20% to 60% of firm value) increases the riskiness of the firm's equity. Accordingly, the equity beta goes up from 1.5 to 2.3.

If we use the simplified approach and set β_D = 0, the result is as follows: 

\( \beta_{A, simplified} = \beta_E \times \frac{E}{D+E} = 1.5 \times 0.8 = 1.2 \).

And the relevered beta, consequently is 3:

\( \beta_{E, simplified}^* = \beta_A \times \big(\frac{D+E}{E}\big)^* = 1.2 \times \big(\frac{1}{0.4}\big) = 3 \).

While the simplified version is computationally less challenging, we see that the resulting relevered beta differs substantially from the value we get when using the "correct" equations. 

More generally speaking, using the simplified equations will lead to a systematic bias in the estimation of the cost of capital. We can easily avoid this bias by switching to the slightly more complicating (but correct) equations. These equations are also implemented in an Excel file, which can be downloaded here. In this file, you can also easily assess the bias you have to accept when working with the simplified equations.