Lektüre: Barwerte (Present Values)

Im letzten Schritt dieses Abschnitts zeigen wir, wie man den Present Value einer Reihe zukünftiger Cashflows berechnet. Auch hier ist die grundlegende Logik dieselbe wie bei den Zukunftswerten. Unter Anwendung des Prinzips der Wertadditivität berechnen wir den Gegenwartswert einer Cashflow-Kette als Summe der Gegenwartswerte der einzelnen Cashflows.

Von zuvor wissen wir, dass der Present Value eines beliebigen zukünftigen Cashflows (C_t) wie folgt berechnet werden kann:

\( \bf{PV_0 = \frac{C_t}{(1+R)^t}} \) 

Folglich ist die Summe des Gegenwartswerts jedes einzelnen Cashflows zwischen dem Zeitpunkt 0 und T gleich:

\( \bf{PV_0 = C_0 + \frac{C_1}{(1+R)}+\frac{C_2}{(1+R)^2}+\frac{C_3}{(1+R)^3}+...+\frac{C_T}{(1+R)^T}} \)

Unter Verwendung des Summenzeichens \( \sum \) können wir schreiben:

\( \bf{PV_0 = \sum_{t=0}^{T} \frac{C_t}{(1+R)^t}} \)

Beispiel 6

Eine Investition verspricht einen Cashflow von 5'000 in 2 Jahren und einen Cashflow von 10'000 in 5 Jahren. Eine alternative Anlage mit gleichem Risiko bringt eine jährliche Rendite von 8%. Wie hoch ist der Gegenwartswert des Investitionsvorschlags basierend auf diesen Informationen?

Die folgende Grafik veranschaulicht den Investitionsvorschlag und dessen Bewertung: 

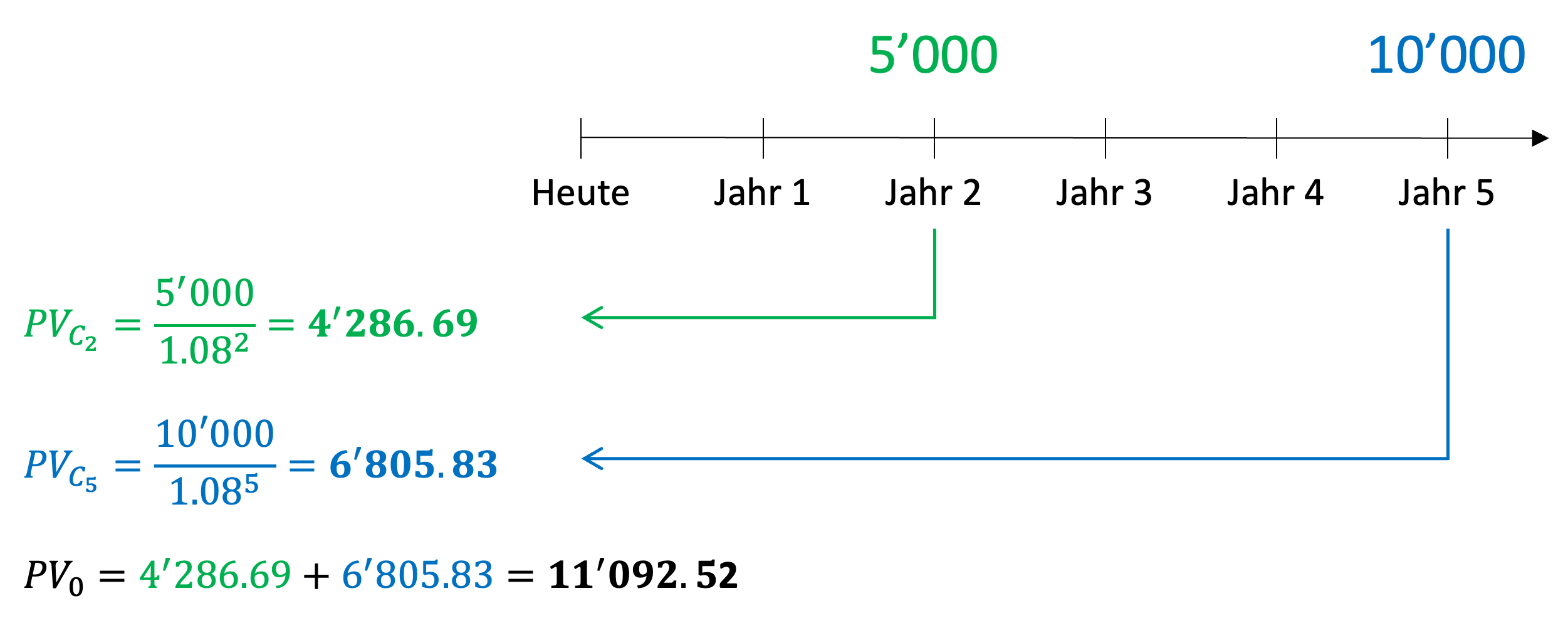
In Worten:

• Der erste Cashflow von 5'000 fällt in 2 Jahren an (C₂). Bei einem Diskontsatz von 8% beträgt sein Present Value 4'286.69.

• Der gleichen Logik folgend hat der zweite Cashflow von 10'000 im Jahr 5 (C₅) einen Present Value von 6'805.83.

• Unter Anwendung des Prinzips der Wertadditivität beträgt der Gesamtwert des Investitionsvorschlags somit 11'092.52.

Warum genau beträgt der Wert des Investitionsvorschlags 11'092.52? Weil dies der Geldbetrag ist, den wir zum Opportunitätszinssatz von 8% investieren müssen, um die Cashflows des Investitionsvorschlags (bei gleichem Risiko) exakt zu replizieren.

Anders ausgedrückt: Anstatt den Investitionsvorschlag zu nehmen, könnten wir 11'092.52 in die alternative Anlage investieren und so in 2 Jahren einen Cashflow von 5'000 und in 5 Jahren einen weiteren Cashflow von 10'000 generieren. Die folgende Tabelle veranschaulicht diese Replikationsstrategie (siehe auch die beigefügte Excel Datei):

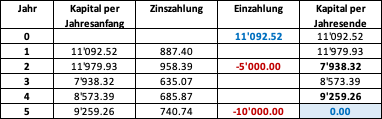
Ähnlich wie im Abschnitt über die Future Values zeigt die Tabelle die Entwicklung einer Investition von 11'092.52 von Jahr zu Jahr bei einer Rendite von 8% und den beschriebenen Cashflows:

• Gemäss dem obigen Investitionsvorschlag entnehmen wir am Ende des Jahres 2 5'000 und am Ende des Jahres 5 10'000.
   
• Wie die Tabelle zeigt, wird der Kontostand nach der zweiten Entnahme genau 0 betragen.
   
• Anders ausgedrückt: Mit der Investition von 11'092.52 in den alternativen Vermögenswert können wir die Cashflows des Investitionsvorschlags exakt replizieren.

Da der ursprüngliche Anlagevorschlag und das Replikationsportfolio die gleichen Cashflows versprechen und das gleiche Risiko aufweisen (gemäss unseren Annahmen), müssen ihre Werte identisch sein. Wir würden daher empfehlen, mit dem Investitionsvorschlag fortzufahren, wenn sein Preis kleiner als 11'092.52 ist. Andernfalls ist es besser, in den alternativen Vermögenswert zu investieren.

Beispiel 7

Ein Investitionsvorschlag verspricht einen Cashflow von 10'000 in 6 Monaten und einen weiteren Cashflow von 10'000 in 1 Jahr. Der Kapitalkostensatz beträgt 10%. Wie hoch ist der Present Value der künftigen Cashflows des Projekts basierend auf diesen Informationen? 

Das Besondere an diesem Beispiel ist, dass der erste Cashflow im Laufe des Jahres und nicht am Ende des Jahres eintritt. Das stellt jedoch kein Bewertungsproblem dar: Wenn der erste Cashflow bereits nach 6 Monaten eintritt, diskontieren wir diesen Cashflow einfach über 6 Monate (= 0.5 Jahre) statt über ein ganzes Jahr. Folglich:

\( PV_0 = \frac{C_{0.5}}{(1+R)^{0.5}}+\frac{C_1}{(1+R)}=\frac{10'000}{1.1^{0.5}}+\frac{10'000}{1.1}= 18'625.53 \)

Der Present Value der zukünftigen Cashflows des Projekts ist folglich 18'625.53.