Reading: Present Values

You are considering an investment proposal with the following expected cash flows:

Alternatively you can invest in an asset with identical risk that promises a rate of return of 10% per year. Based on this information, what is the Present Value of the investment proposal?

There are various ways to compute the present value of this cash flow string. First, we can explicitly write down the present value formula and then compute it manually. The result is:

\( PV_0 = -1000 + \frac{1'000}{1.1} +\frac{2'000}{1.1^2} +\frac{3'000}{1.1^3} +\frac{4'000}{1.1^4} +\frac{5'000}{1.1^5} = 9'652.59 \)

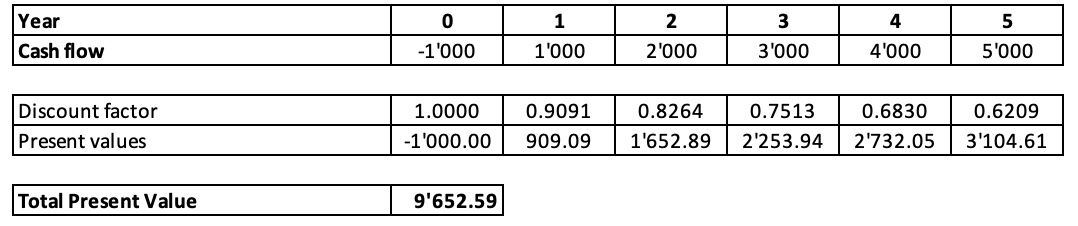
Alternatively, we can go back to the table with discount factors and apply the relevant discount factor to the corresponding cash flow. The result is shown in the table below, as well as in the accompanying Excel file.

For example, for year 1, the discount factor is 0.9091, so that the present value of C₁ is 1'000 × 0.9091 = 909.09. Similarly, the discount factor for C₂ is 0.8264, so that the present value of C₂ is 2'000 × 0.8264 = 1'652.89. Etc. As the last row of the table shows, the overall value of the individual present values is 9'652.59, which is, not surprisingly, the same result as with the preceding manual method.

Finally, an elegant way to compute the present value of longer cash flow series is the Excel function "NPV", which integrates the whole computation in a sigle table cell.  The accompanying Excel file also contains this alternative way to estimate the NPV (which is shown in cell C12). For a more detailed discussion on how to implement that function, please refer to the document Practical Tips for Excel's NPV Function.