Reading: Internal Rate of Return (IRR)

Let's start with a simple example.

Example 1

Suppose you can invest 1'000 today in a project that is expected to generate a payoff of 1'300 in 1 year. Based on this information, what return can investors expect to earn with this project?

With such a one period investment proposal, the project return can be computed fairly easily:

\( \text{Return (%)} = \frac{\text{Payoff}}{\text{Investment}} - 1 = \frac{1'300}{1'000} -1 = 0.3 = 30\% \)

Investors can expect to earn a rate of return of 30%. This is the project's internal rate of return (IRR). Investors now have to assess whether this IRR is sufficient in light of the riskiness of the project. Put differently, they have to compare the project IRR with the cost of capital:

• If the IRR is larger than the cost of capital, investors earn a higher return with the project than they can earn elsewhere (at the same risk). They should therefore invest.
   
• In contrast, if the IRR is smaller than the cost of capital, the project return is insufficient to cover the cost of capital. Investors should therefore not invest.

The IRR therefore allows us to express the project's value added as a rate of return instead of a currency amount. This allows us to rephrase the NPV rule as follows:

IRR rule: Accept investment proposals that offer IRRs in excess of the cost of capital.

The difference between the IRR and the cost of capital is sometimes also referred to as the return spread:

Return spread = IRR − Cost of Capital.

For normal investment projects, a positive return spread implies that the project also has positive NPV.

If the IRR is just equal to the cost of capital, the project offers exactly the investors' expected rate of return. The project NPV will therefore be zero. Consequently, we can write down the standard expression for the NPV calculation and find the discount rate that leads to a NPV of zero. Using the notation from the preceding section:

\( NPV = -C_0 + \frac{C_1}{1+IRR} = 0 \)

In our example from before, the discount rate in question is 30%: 

\( IRR = \frac{C_1}{C_0}-1 = \frac{1'300}{1'000} - 1 = 0.3 = 30\% \)

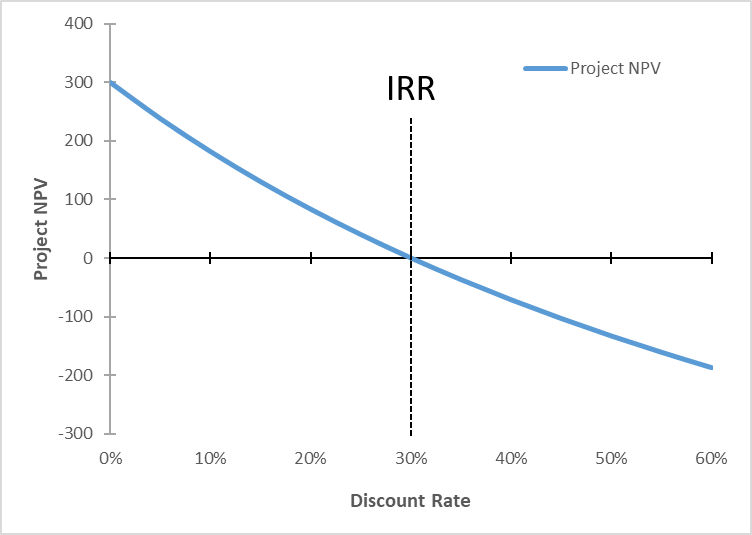
As long as the appropriate discount rate is smaller than 30%, the project NPV is positive and we should take it. The following graph illustrates this. It depicts the NPV of the project from Example 1 (vertical axis) as a function of the discount rate (horizontal axis):

• As the discount rate increases, the present value of C₁ drops, and so does the project NPV.
• At a discount rate of 30%, the NPV is just zero. That's the IRR of the project.
• At discount rates in excess of 30%, the project NPV is negative. For example, if the discount rate is 40%, the project NPV drops to −71.4 [= 1'000 + 1'300/1.4].