Lektüre: Internal Rate of Return (IRR)

Beginnen wir mit einem einfachen Beispiel:

Beispiel 1

Nehmen wir an, Sie können heute 1'000 in ein Projekt investieren, das in einem Jahr eine Auszahlung von 1'300 verspricht. Welche Rendite können Anleger mit diesem Projekt erwarten?

Bei einem derart einfachen Projekt, das nur über ein Jahr läuft, ist die Berechnung der Projektrendite keine grosse Herausforderung:

\( \text{Rendite (%)} = \frac{\text{Auszahlung}}{\text{Investition}} - 1 = \frac{1'300}{1'000} -1 = 0.3 = 30\% \)

Die Investoren können mit einer Rendite von 30% rechnen. Dies ist der interne Zinsfuss (Internal Rate of Return, IRR) des Projekts. Die Investoren müssen nun beurteilen, ob dieser IRR angesichts des Risikos des Projekts ausreichend ist. Anders ausgedrückt: Sie müssen den IRR des Projekts mit den Kapitalkosten vergleichen: 

• Wenn der IRR größer ist als die Kapitalkosten, erzielen die Investoren mit dem Projekt eine höhere Rendite als sie anderswo (bei gleichem Risiko) erzielen können. Sie sollten daher investieren.

• Ist der IRR dagegen kleiner als die Kapitalkosten, reicht die Projektrendite nicht aus, um die Kapitalkosten zu decken. Die Investoren sollten daher nicht investieren.

Der IRR ermöglicht es uns also, den (finanziellen) Mehrwert des Projekts als Rendite statt als Geldbetrag auszudrücken. Damit lässt sich die NPV-Regel wie folgt umformulieren:

IRR-Regel: In Projekte investieren, deren IRR höher ist als die Kapitalkosten

Die Differenz zwischen dem IRR und den Kapitalkosten wird manchmal auch als Renditespanne (engl. Return Spread) bezeichnet:

Renditespanne = IRR − Kapitalkosten.

Bei normalen Investitionsprojekten bedeutet eine positive Renditespanne, dass das Projekt auch einen positiven NPV hat.

Wenn der IRR gerade gleich den Kapitalkosten entspricht, bietet das Projekt genau die von den Investoren erwartete Rendite. Der NPV des Projekts ist dann gleich Null. Folglich können wir den Standardausdruck für die NPV-Berechnung aufschreiben und den Diskontsatz finden, der zu einem NPV von Null führt. Mit der Notation aus dem vorangegangenen Abschnitt können wir schreiben:

\( NPV = -C_0 + \frac{C_1}{1+IRR} = 0 \)

In unserem vorangehenden Beispiel ist der gesuchte Diskontsatz 30%: 

\( IRR = \frac{C_1}{C_0}-1 = \frac{1'300}{1'000} - 1 = 0.3 = 30\% \)

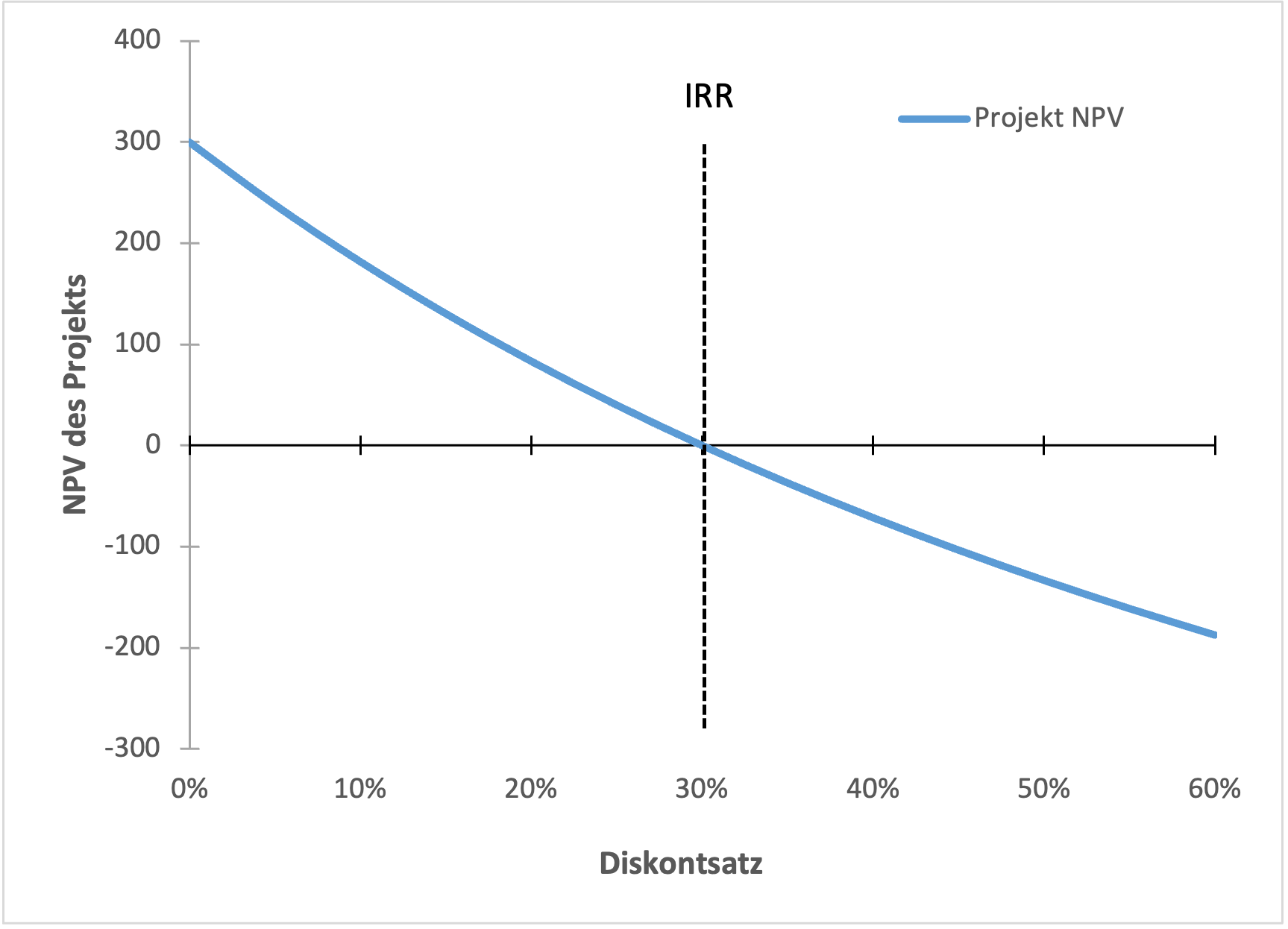
Solange der für das Projekt angemessene Diskontsatz unter 30 % liegt, ist der NPV des Projekts positiv und wir sollten es annehmen. Die folgende Grafik veranschaulicht dies. Es zeigt den NPV des Projekts aus Beispiel 1 (vertikale Achse) als Funktion des Diskontsatzes (horizontale Achse):

• Mit steigendem Diskontsatz sinkt der Gegenwartswert von C₁ und damit auch der Kapitalwert des Projekts.
• Bei einem Diskontsatz von 30% ist der NPV gleich Null. Das ist der IRR des Projekts.
• Bei Diskontsätzen von mehr als 30% ist der NPV des Projekts negativ. Beträgt der Diskontsatz beispielsweise 40%, sinkt der Kapitalwert des Projekts auf -71.4 [= 1'000 + 1'300/1.4].