Lektüre: Internal Rate of Return (IRR)

Das vorangegangene Beispiel 1 hat gezeigt, wie der IRR eines Investitionsprojekts, das nur eine Periode dauert, berechnet und interpretiert werden kann. Aber wie berechnet man den IRR eines mehrperiodigen Projekts? Hier wird die Mathematik etwas komplizierter... Erinnern wir uns daran, dass der IRR dem Diskontsatz entspricht, der den NPV des Projekts auf Null setzt. Wir können daher die Berechnung des IRR für ein Projekt mit einer Dauer von T Perioden wie folgt verallgemeinern:

\( NPV = C_0 + \frac{C_1}{(1+IRR)}+ \frac{C_2}{(1+IRR)^2}+...+ \frac{C_T}{(1+IRR)^T} = 0 \)

Um den IRR des Projekts zu ermitteln, müssten wir den obigen Ausdruck nach der Variable IRR auflösen, was sehr schwierig, oft nicht eindeutig und manchmal sogar unmöglich ist. Daher wird die IRR-Berechnung in der Praxis oft durch ein "Trial-and-Error"-Verfahren oder mit Tabellenkalkulationsprogrammen wie Microsoft Excel durchgeführt.

Beispiel 2

Betrachten wir ein Projekt, das die folgenden Cashflows verspricht:

Welchen IRR hat das Projekt?

"Trial-and-Error"-Verfahren

Um das Problem mittels "Trial-and-Error"-Verfahren zu lösen, würden wir einfach verschiedene Diskontsätze verwenden, um die Cashflows des Projekts zu kapitalisieren. Auf diese Weise könnten wir schliesslich den IRR des Projekts iterativ ermitteln. Wir könnten zum Beispiel mit einem Diskontsatz von 10% beginnen und den entsprechenden Kapitalwert des Projekts von 892.6 % berechnen:
  

\( NPV_{10\%} = -12'000+\frac{6'000}{1.1}+\frac{9'000}{1.1^2} = 892.6 \)

 
Da der NPV bei einem Diskontsatz von 10% noch positiv ist, muss der IRR des Projektes höher als 10% sein. In einem zweiten Schritt könnten wir das Projekt deshalb beispielsweise mit einem Diskontsatz von 20% bewerten, wobei ein NPV von −750 resultieren würde:

\( NPV_{20\%} = -12'000+\frac{6'000}{1.2}+\frac{9'000}{1.2^2} = -750.0 \)

Da dieser NPV jetzt negativ ist, wissen wir, dass der IRR kleiner als 20%, aber größer als 10% sein muss. Beim nächsten Versuch sollte also ein Diskontsatz zwischen 10 % und 20 % gewählt werden, usw. Nach vielen Versuchen würden wir herausfinden, dass der NPV des Projekts genau Null ist, wenn wir die zukünftigen Cashflows mit einem Diskontsatz von 15.1 % abzinsen:

\( NPV_{15.1\%} = -12'000+\frac{6'000}{1.151}+\frac{9'000}{1.151^2} = 0 \)

Der IRR des Projekts ist deshalb 15.1%. Ausgerüstet mit diesem Wissen können die Investoren nun entscheiden, ob eine jährliche erwartete Rendite von 15.1% ausreichend ist, angesichts des Risikos des Projekts.

Es liegt auf der Hand, dass das "Trial-and-Error"-Verfahren keine ausgesprochen elegante Methode zur Lösung dieses Problems ist. Viel effizienter und exakter ist Verwendung der "IKV"-Funktion in Excel (IRR in der englischsprachigen Version von Excel).

Die "IKV"-Funktion von Excel

Microsoft Excel verfügt über eine integrierte Funktion "IKV", mit der sich der IRR eines Projekts leicht berechnen lässt. Die Funktion lässt sich in der gewünschten Ausgabezelle von Excel wie folgt abrufen:
 

=IKV(

dann markieren Sie einfach den fraglichen Cashflow-Strom, schliessen die Klammern und drücken die Eingabetaste. Excel zeigt uns nun den IRR an, der den NPV des Cashflow-Stroms gleich Null setzt. 

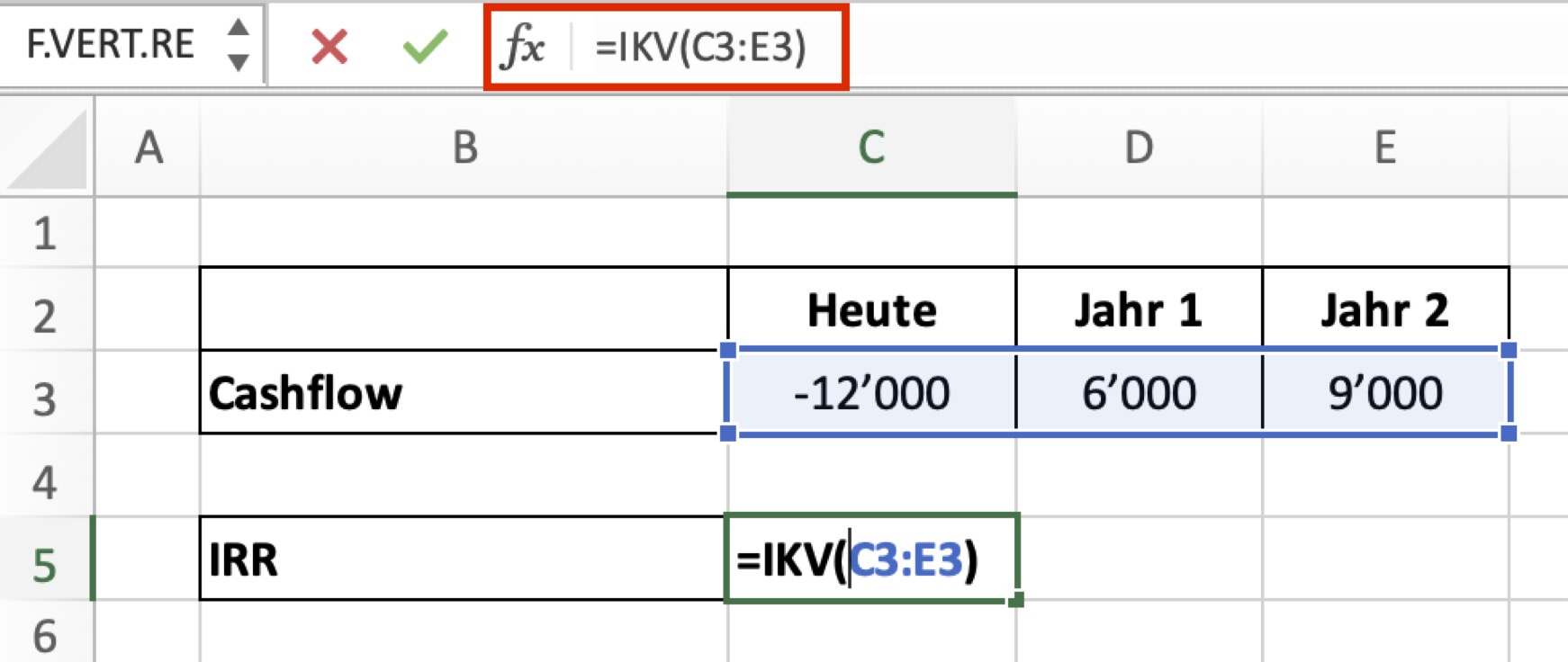
Der folgende Bildschirmausschnitt von Excel veranschaulicht dies:

• Die relevanten Cashflows des Projekts sind in den Zellen C3 bis E3
• Wir wollen, das Excel den IRR in Zelle C5 berechnet
• Um den IRR zu berechnen, schreiben wir in Zelle C5: =IKV(C3:E3). Dies sagt Excel, dass es den IRR  eines Zahlungsstromes berechnen soll, der von C3 bis E3 läuft.
• Das Resultat ist ein IRR von 15.1%.

Sobald wir die Cashflows in Excel hergeleitet haben, ist es daher nur noch ein kleiner Schritt, deren IRR zu berechnen. Da es so einfach ist, den IRR zu berechnen, und da dieser so aussagekräftig ist, sollten wir ihn bei der Präsentation sämtlicher Investitionsvorschläge mitberücksichtigen.