Reading: Internal Rate of Return (IRR)

Before, we have mentioned that it is not always easy to determine whether a proposal has the characteristics of a borrowing project or a lending project. The reason is that specific projects could be a mixture of borrowing and lending. This will pose challenges to the IRR rule, as the following example shows:

Example 4

Consider Project C with the following cash flows. Should we invest in the project?

When we compute Project C's IRR in Excel, the result is IRR = 13.7%. A quick check shows that the project NPV is indeed 0 if the discount rate equals 13.7%:

\( NPV_{13.7\%} = -5'000 + \frac{13'600}{1.137} - \frac{9'000}{1.137^2} = 0 \)

But how to interpret this IRR? Suppose the cost of capital is 10%. Should we now take the project because its IRR is higher than 10% and we believe Project C has the characteristics of an investment project? Or should we discard the project because Project C is a borrowing project, in which case it would be cheaper to borrow at the market rate of 10%?

These questions arise because the project has a particular cash flow pattern. It starts and ends with cash outflows and has a considerable cash inflow in between. Such a cash flow pattern could be typical for projects that have significant dismantling costs at the end of their life. Take, for example, a nuclear power plant. At project end, such a plant cannot be simply switched off and everybody walks away. Decommissioning such a plant can take years and cost hundreds of millions of dollars. A case in point is the Yankee Nuclear Power Plant in Massachusetts, whose decommissioning took 15 years and cost more than $600 million.

Going back to Project C, we can already see that, at a discount rate of 0%, the NPV is negative: If the cost of capital is zero, the NPV of the project corresponds to the sum of its cash flows, which is −400 in the case of project C [= −5'000 + 13'600 − 9'000]. Similarly, it is conceivable that at very high discount rates, the present value of all future cash flows will be so small that they cannot justify today's investment. The question therefore is whether the project NPV is negative throughout, or whether there is a range of discount rates that result in a positive NPV.

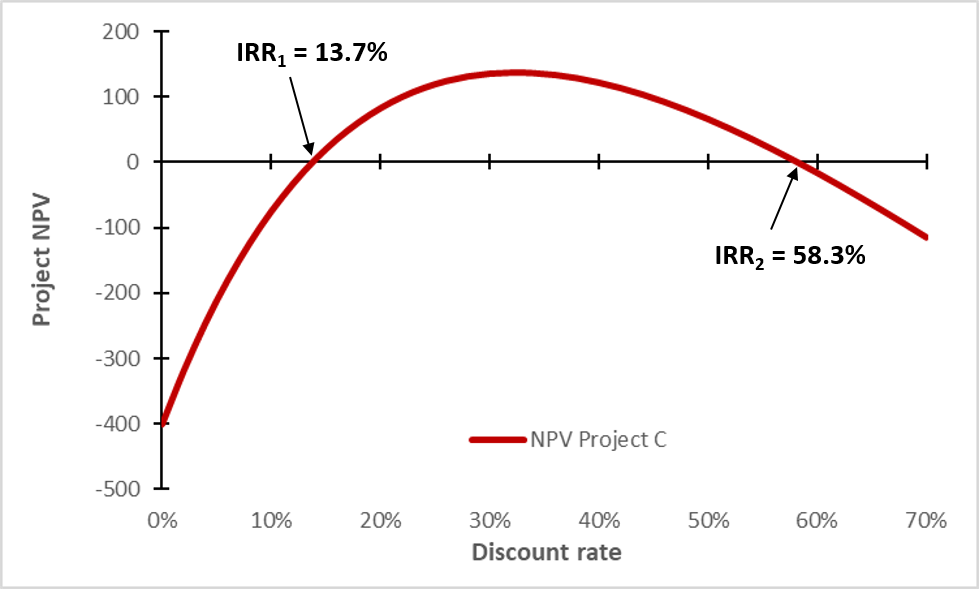
To answer this question, we can draw the NPV profile of Project C as a function of the discount rate:

It turns out that the project has two IRRs: IRR₁ is 13.7% (see before) and IRR₂ is 58.3%. If the actual discount rate is somewhere between 13.7% and 58.3%, the project adds value and we should pursue it. At a lower or higher cost of capital, however, the project NPV is negative!

By simply looking at the cash flows and the IRR, it is very difficult to come up with a reliable investment decision for project C. The problem arises because the cash flow stream switches signs twice. Theoretically, a project can have as many IRRs as algebraic sign switches. For projects with such alternating cash flow directions, we should therefore be particularly careful when using the IRR.