Reading: Internal Rate of Return (IRR)

In many real life situations, projects have multiple alternatives and the available resources have different uses. For example, a real estate developer could choose between residential and commercial use of a newly acquired plot. By choosing one alternative, the developer decides against other potential uses. Put differently, the project alternatives are mutually exclusive. In such valuation situations, the IRR rule can be misleading.

Example 6

Suppose we have to choose between the following two mutually exclusive projects. Which one should we pick, assuming that the cost of capital is 10%?

Based on the IRR rule, we would opt for Project E, since its IRR of 38% is considerably larger than that of Project F (22%). But is Project E really better? While its IRR is larger, the project itself is much smaller. Therefore, if we opt for Project E, we earn a high return on a comparatively small investment. Would it be financially more attractive to earn a smaller return on a much larger investment?

The IRR rule cannot answer this question. To find an answer, we can turn to the NPV criterion, which clearly indicates that we should choose project F (remember that the assumed cost of capital is 10%):

\( NPV_E = -1'000 + \frac{800}{1.1} + \frac{800}{1.1^2} = 388 \)

\( NPV_F = -15'000 + \frac{10'000}{1.1} + \frac{10'000}{1.1^2} = 2'355 \)

If Projects E and F are the only available investment opportunities, we should go with Project F because it puts more money to work. As a result, its NPV of 2'355 is considerably larger than that of Project E (388).

The standard IRR rule ignores the size of the project. Therefore, whenever we are dealing with project alternatives that have strikingly different investment requirements, it fails to provide a complete answer. The NPV rule does not fall pray to that problem. We should therefore report the IRR always together with the NPV.  

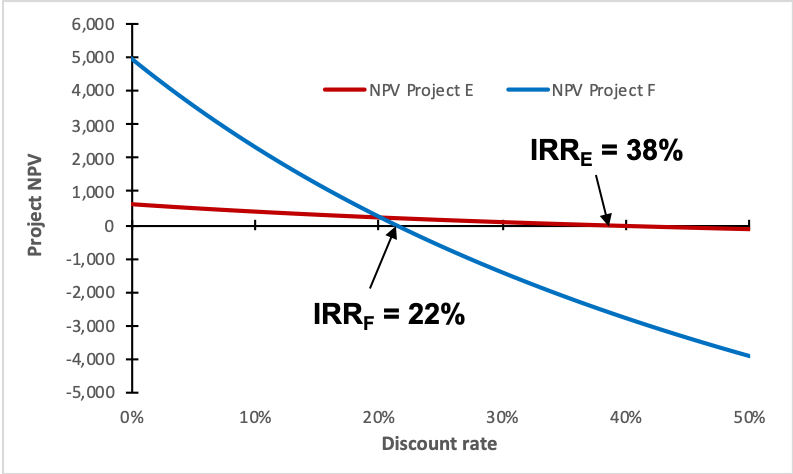
If we have no estimate of the appropriate cost of capital, we can draw the NPV-profile as a function of the discount rate:

This profile clearly shows that Project F is preferable if the cost of capital is lower than approximately 20%. Only if the cost of capital exceeds 20%, we should opt for Project E. If the cost of capital is larger than 38%, we should not invest at all.

IRR of Incremental Cash Flows

In principle, it is also possible to adjust the IRR rule so that it can handle investment decisions that involve mutually exclusive projects with different scale. Here is how it works:

• Start the analysis with the smaller project that has the higher IRR (if the larger project alternative has a higher IRR, then you should obviously go for that alternative).
• Then look at the additional cash flows that the larger project offers
• Compute the IRR (and NPV) of these incremental cash flows. If the IRR of the incremental cash flows exceed the cost of capital, you know that it is worthwhile to make the additional investment and you should opt for the larger project.

In the case of Example 6, the incremental cash flows of Project E are:

• Additional investment of 14'000 today
• Additional cash inflows of 9'200 in years 1 and 2:

The IRR of this incremental cash flow stream is 20%:

\( NPV_{20\%} = -14'000 + \frac{9'200}{1.2} + \frac{9'200}{1.1^2} = 0 \)

Assuming a cost of capital of 10%, the return we can earn on the additional investment is therefore well in excess of the cost of capital. We should therefore choose Project F instead of Project E.

Example 7

You can choose between the following two projects G and H. Which one do you choose based on the IRR rule if the cost of capital is 10%?

Project G has the higher IRR than Project H (32% vs. 22%) but it is also somewhat smaller (initial investment of 12'000 vs. 15'000). Following up on the discussion in Example 6, the question is whether the additional investment of 3'000 that is associated with project H will earn a return in excess of the cost of capital.

The answer is clearly no. As the table above shows, project H only generates an additional cash inflow of 1'000 per year. The IRR of these additional cash flows is -23.24%. Compared with Project G, Project H therefore destroys value. We should opt for project G.

This is also the answer we get when considering the NPV rule (remember that we assume a cost of capital of 10%):

\( NPV_G = -12'000 + \frac{9'000}{1.1} + \frac{9'000}{1.1^2} = 3'620 \)

\( NPV_H = -15'000 + \frac{10'000}{1.1} + \frac{10'000}{1.1^2} = 2'355 \)

The NPV of project G exceeds that of project H by 1'265. The NPV rule therefore tells us to take project G.

Different Investment Horizons

The preceding examples have shown that the IRR rule is unreliable when dealing with projects of different scale. The same is true when it comes to projects with different investment horizons, as the following example shows.

Example 8

Consider the following two projects I and J. Which one would you choose based on the IRR rule if the cost of capital is 10%?

Both projects require the same initial investment of 12'000 today. Project I then runs for 2 years and generates an IRR of 32%. In contrast, Project J runs for 5 years and generates an IRR of 25%. Consequently, the standard IRR rule would tell us to go with Project I. But is Project I really better? Put differently, is it better to earn 32% per year over 2 years when we can earn 25% per year over 5 years? The standard IRR rule does not provide an answer.

To find an answer, we can compute the NPVs of the two projects or we can analyze the incremental IRR of Project J compared with Project I. Both analyses yield the same result: We are financially better off when we choose Project J, i.e., the one with the lower return over the longer investment period. The NPV of Project J is 1'439 higher (5'059 vs. 3'620):

\( NPV_I = -12'000 + \frac{9'000}{1.1} + \frac{9'000}{1.1^2} = 3'620 \)

\( NPV_J = -12'000 + \frac{4'500}{1.1} + \frac{4'500}{1.1^2}+...+\frac{4'500}{1.1^5} = 5'059 \)

And the IRR of its incremental cash flows is 18% and therefore well beyond the cost of capital:

As this example shows, the standard IRR rule can therefore be misleading when assessing projects with different investment horizons.

Interestingly, many practitioners will argue that Project I is still better than J, because it returns the capital more quickly. This capital is then available for reinvestment in new projects with positive NPV. While this argument is, in principle, valid, it is based on a fundamentally different investment scenario than the one that we have considered in example 8:

• First, it assumes the existence of additional projects with positive NPV that can be launched at a later point in time (in, say, 3 years). 
• Second, it assumes that the new project (or projects) is incompatible with project J and can only be launched in combination with I.
• And third, it also assumes some sort of financial constraints, such that we have to wait for the payoffs of Project I in order to have sufficient funds available to launch Project K.

With these additional assumptions, it could well be that Project I turns out to be more valuable than Project J. Without, it is clearly not. Importantly, the assumption of financing constraints is questionable for many mature firms. These firms often generate more cash from existing projects than they can reinvest into new projects. The massive buyback and payout programs that we are witnessing are a clear indication of this lack of investment opportunities (see the module Payout Policy).

And even if there are financing constraints, the IRR rule will generally be unable to identify the best investment strategy within these constraints.