Reading: From Value to Issue Price

The previous sections have discussed important valuation issues in the context of startup companies. Let us now assume that we have "found" a fair exit value and that the entrepreneur as well as the investors agree on this valuation. In the separate module Deal Structuring, we will then show how we can make deals possible even if the buyers and sellers cannot agree on a valuation.

The next task we face is to get from the valuation to the actual price at which an investor can buy new shares. That's the topic of this section. To illustrate, let's go back to the hypothetical company that we have considered at the beginning of the previous section. The company had the following characteristics:

• Exit value in 5 years: 180 million
• Investor's required rate of return (hurdle rate): 40%
• Present value of exit value: 33.5 million
• Required capital: 6.7 million
• Let us also assume that the firm currently has 100'000 shares outstanding, all of which are issued to the entrepreneur.

Since the present value of the exit value (33.5 million) is considerably higher than the required capital (6.7 million), we have concluded that the company looks like a financially attractive investment opportunity. 

Now let us look at some important terminology:

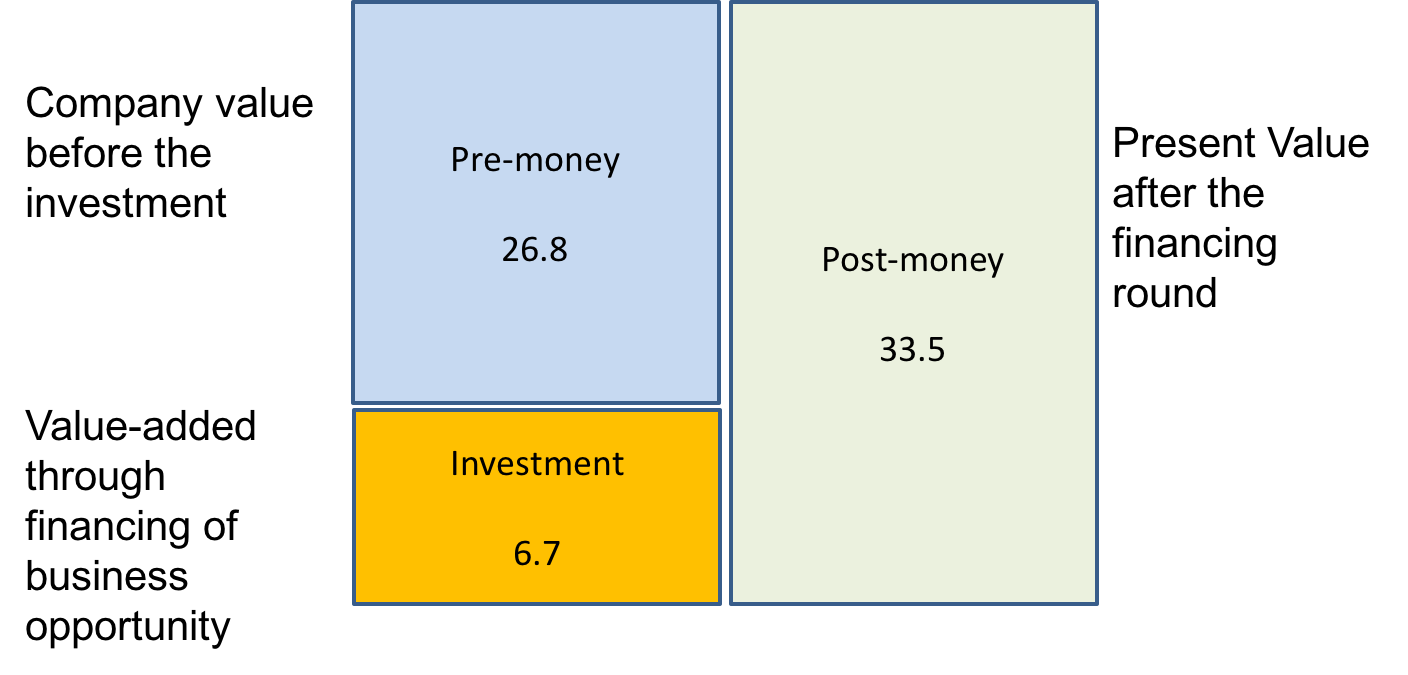
• The firm's valuation of 33.5 million is the so-called post-money valuation. Why post money? Because the firm needs the capital investment of 6.7 million to be able to reach the exit. Put differently, this value can only be achieved if the investors actually invest in the company.
• The pre-money valuation, in turn reflects the value of the company before the capital investment. Under the assumption that there is sufficiently large competition among investors, the investors will end up covering their expected cost of capital without capturing any value-added of the company. Hence, the pre-money valuation corresponds to the post-money valuation net of the capital contribution:
   
  Pre-money valuation = Post-money valuation - Capital needs = 33.5 - 6.7 = 26.8 million.
   
• The pre-money valuation is positive, which implies that the company seems to be an interesting investment.

The following graph summarises the relation between pre-money and post-money valuation:

VC's Required Ownership Stake

So far we have looked at the whole firm. But the entrepreneurs will not give the investors the whole firm in return for their investment. Instead, the investors will receive a fraction of the ownership. Our next task is to determine what fractional ownership the investors will require in return for their investment of 6.7 million.

The investors will want to make sure that their ownership stake has at least a value of 6.7 million. Put differently:

f_VC × Post-money valuation ≥ Invested capital,

where f_VC denotes the fractional ownership (in %) that the investors will require. We can solve this expression for f_VC and find:

\( f_{VC} \geq \frac{\text{Invested capital}}{\text{Post-money valuation}} = \frac{6.7}{33.5} \) = 20%. 

Consequently, the investors will require an ownership stake of at least 20% in exchange for their investment of 6.7 million. In our previous considerations about the pre-money and the post-money valuation, we have assumed that the capital market is fairly competitive so that the investors just cover their cost of capital. Under this assumption, the investors will get exactly 20% of the company's equity and earn the required return of 40% per year.

The Number of Newly Issued Shares

The next question is how the investors can actually receive an ownership stake of 20%. Given that the firm has 100'000 shares outstanding (see above), the quick and intuitive answer would be to assume that the investors will get 20'000 shares, i.e., 20% of the current number of shares outstanding. This answer is generally wrong, however. Why? Because the 100'000 shares the firm currently has are all owned by the entrepreneur. If the company needs capital, it will be the company that sells shares to the investor, and not the entrepreneur! Put differently, the company will have to issue new shares. But how many? We can find the answer as follows:

• If the VC owns 20% of the shares after the transaction, the remaining shareholders (in our case the entrepreneur) will own 80% of the shares outstanding.
• Put differently, the 100'000 shares the entrepreneur currently owns will reflect 80% of all shares.
• Consequently, the total number of shares outstanding after the transaction will be 100'000/0.8 = 125'000.
• This implies that the investor will receive 25'000 shares, i.e., the difference between the number of shares outstanding before and after the transaction.
• So after the transaction, there will be 125'000 shares outstanding, of which 100'000 (80%) will be controlled by the entrepreneur and 25'000 (20%) by the investor.

We can reach the same conclusion more formally: The investor wants to make sure that the newly issued shares account for 20% of the current plus the newly issued shares:

Newly issued shares = f_VC × (Current number of shares + Newly issued shares).

Now we can rearrange this expression to find the number of newly issued shares:

Newly issued shares = Current number of shares × \( \frac{f_{VC}}{(1-f_{VC})} = 100'000 \times \frac{0.2}{(1-0.2)} = 25'000 \).

Consequently, the total number of shares outstanding after the transaction will be 100'000 + 25'000 = 125'000.

The Issue Price

Now we are ready to compute the price at which the investors will be able to buy shares, the so-called issue price. Remember that the investors provide an investment of 6.7 million and receive 25'000 shares in return. Consequently, the implied issue price is 268:

Issue price = \( \frac{\text{Capital invested}}{\text{Newly issued shares}} = \frac{6'700'000}{25'000} = 268 \).

We have seen the basic mechanics that help us get from the valuation of the firm to the actual price the investor will have to pay for the newly issued shares. The result was as follows:

• In exchange for his investment of 6.7 million, the investors require a share in capital of 20%
• Given that there are currently 100'000 shares outstanding, the firm will have to issue 25'000 new shares to the investors
• If the capital infusion of 6.7 million buys 25'000 shares, the implied price per share is 268.

Under this deal structure, the investors expect to earn a return that exactly corresponds to their hurdle rate of 40%. To see this, we can conduct the following computations:

• Today, the issue price of the shares is 268 each.
• In 7 years, the expected exit value is 180 million (see above)
• If there are 125'000 shares outstanding, the expected share price at the time of exit is 180'000'000/125'000 = 1'440.
• Put differently, the investor expects that during the investment period of 5 years, the stock price increases from 268 (issue price) to 1'440 (expected exit price). 
• The expected return, therefore is 40%, which exactly corresponds to the investor's hurdle rate:
   
  Expected return = \( (\frac{\text{Expected exit price}}{\text{Issue price}})^{0.2}-1 =(\frac{1'440}{268})^{0.2}-1 \) = 40%.

Ownerhsip Dilution

Another noteworthy point that follows directly from the previous considerations is that such financing rounds affect the ownerhip stake of the current shareholders (in our example the entrepreneur). While the numbers of shares outstanding increases from 100'000 to 125'000, the entrepreneur owns the same number of shares before and after the financing round (100'000). Consequently, his ownership stake drops from 100% to 80%. 

This effect is called dilution. More generally speaking, if a shareholder does not participate in a future round of financing (or does not do so proportionally to his current ownership stake), his fractional ownership in the company will decrease. This can have far-reaching implications on the control structure of the company and, of course, also the valuation of the shares.

Potential ownership dilution could also be a concern for the investor. We will address this concern in the following section.