Lektüre: Barwerte (Present Values)
6. Übungsbeispiel
Sie erwägen einen Investitionsvorschlag mit den folgenden erwarteten Zahlungsströmen:
| Jahr | 0 | 1 | 2 | 3 | 4 | 5 |
| Cashflow | -1'000 | 1'000 | 2'000 | 3'000 | 4'000 | 5'000 |
Alternativ können Sie auch in einen Vermögenswert mit demselben Risiko investieren, der eine Rendite von 10% pro Jahr verspricht. Wie hoch ist auf der Grundlage dieser Informationen der Present Value des Investitionsvorschlags?
Es gibt verschiedene Möglichkeiten, den Present Value dieses Cashflow-Musters zu berechnen. Zunächst können wir die Present Value-Formel explizit aufschreiben und dann manuell berechnen. Das Ergebnis lautet:
\( PV_0 = -1'000 + \frac{1'000}{1.1} +\frac{2'000}{1.1^2} +\frac{3'000}{1.1^3} +\frac{4'000}{1.1^4} +\frac{5'000}{1.1^5} = 9'652.59 \)
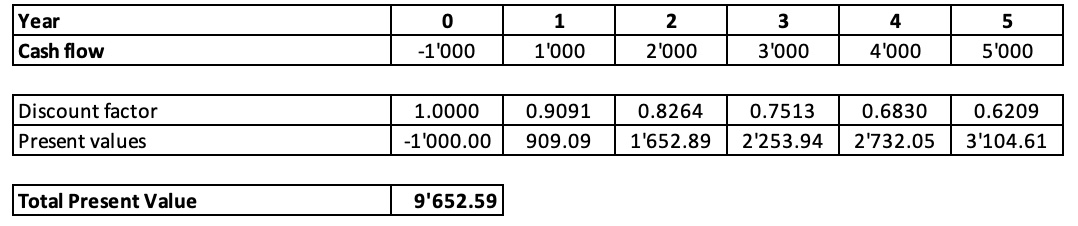
Alternativ können wir auch zurück zur Tabelle mit den Diskontierungsfaktoren gehen und die relevanten Faktoren den entsprechenden Cashflows zuordnen. Das Resultat ist in der folgenden Tabelle zusammengefasst, genauso wie in der beiliegenden Excel-Datei.
Für das Jahr 1 beträgt der Diskontierungsfaktor beispielsweise 0.9091, so dass der Present Value von C1 1'000 × 0.9091 = 909.09 beträgt. Analog dazu beträgt der Diskontierungsfaktor für C2 0.8264, so dass der Present Value von C2 2'000 × 0.8264 = 1'652.89 beträgt. Usw. Wie die letzte Zeile der Tabelle zeigt, beträgt der Gesamtwert der einzelnen Gegenwartswerte 9'652.59, was, wenig überraschend, dasselbe Ergebnis ist wie bei der vorhergehenden manuellen Methode.
Eine elegante Möglichkeit, den Present Value längerer Cashflow-Reihen zu berechnen, ist schliesslich die Excel-Funktion "NBW", die die gesamte Berechnung in eine einzige Tabellenzelle integriert. Die beigefügte Excel-Datei enthält auch diese alternative Methode zur Schätzung des Kapitalwerts (die in Zelle C12 dargestellt ist). Eine ausführlichere Diskussion über die Implementierung dieser Funktion finden Sie in dem Dokument Praktische Tipps für Excel's NBW-Funktion.